Определение опорных реакций балок
На опорах балок возникают реакции, с определения которых следует начинать решения всех задач по расчету изгиба.
Реакции опор определяются из уравнений равновесия (статики), которые можно представить в двух различных вариантах:
1) в виде суммы проекций всех сил на оси х и у , а также суммы моментов сил (включая реакции) относительно любой точки по оси балки:
Уравнения равновесия очень важны, когда речь идет о анализе пучка. Используя эти три уравнения, вы можете узнать неизвестные значения для реакций поддержки, зная силы и длины сегментов луча. Моментное уравнение действительно полезно, потому что оно позволяет вам решить проблему без разложения определенных сил, любая сила, действующая в той же строке, которую вы берете в момент, равна нулю.
Итак, если у вас три неизвестные силы, но 2 из них проходят через одну и ту же точку, то взятие момента в этот момент будет пренебрегать этими силами и изолировать третью сторону в разрешимом уравнении. Шаг 5 Решите для внутренней осевой силы разреза, суммируя все силы, параллельные лучу. Шаг 6 Решите для внутренней силы сдвига срезанной секции, суммируя все усилия, перпендикулярные лучу. Шаг 7 Решите для внутренней силы момента разреза, суммируя внешние моменты силы, а также любые точечные моменты на разрезе.
2) в виде суммы всех сил на одну из координатных осей х или у и двух сумм моментов сил (включая реакции) относительно двух точек, лежащих на оси балки:
Выбор того или оного варианта составления уравнений равновесия, а также выбор точек по направлению координатных осей, используемых при составлении этих уравнений, производится в каждом конкретном случае с таким расчетом, чтобы по возможности не производить совместное решение уравнений. Для проверки правильности определения опорных реакций полученные их величины рекомендуется подставлять в какое-либо уравнение равновесия, не использованное ранее.
Построение диаграмм сдвига и моментов
Шаг 8 Если вы хотите проверить свои решения внутренних сил, используйте заброшенный разрез на шаге 4 и вычислите внутренние силы на шагах 5-7. Вы должны получить тот же ответ. На следующих этапах представлен графический метод построения диаграмм сдвига и момента.
Шаг 1 Нарисуйте диаграмму свободного тела луча и укажите условное соглашение, которое будет использоваться во всем решении. Шаг 2 Решите для всех неизвестных внешних реакций, используя три уравнения равновесия. Шаг 3 После вычисления всех внешних реакций вы можете перейти к диаграмме сдвига. Посмотрите на диаграмму свободного тела, начиная с левой стороны луча. Если в конце нет нагрузки, вы можете перейти к следующему шагу, так как сдвиг в точке равен нулю. Однако, если есть сила, расположенная, то линия может быть оттянута от нуля вплоть до величины сосредоточенной нагрузки.
При определении реакций их направления можно выбирать произвольно. Если же реакции в расчете оказались отрицательными, то это означает, что их направление выбрано неправильно. В этом случае на расчетной схеме первоначальное направление реакций перечеркивают и указывают их обратное направление. В последующих расчетах величины реакций считаются положительными.
Направление точки зависит от того, является ли сила положительной или отрицательной. Шаг 4 Теперь продолжайте смотреть справа от луча, пока вы рисуете горизонтальную линию, пока не будет показано другое значение для нагрузки, если это будет другая точечная нагрузка, тогда вы продолжите с точки, которую вы остановили в предыдущем разделе, и можете добавить или вычесть значение силы в зависимости от ее направления. В конечном итоге вы это сделаете, пока не доберетесь до другой стороны луча. Если бы на пучке была равномерно распределенная нагрузка в зависимости от длины распределения, линия была бы построена по диагонали, связывая положительное и отрицательное значение площади распределенной нагрузки.
Однако можно заранее предугадать правильное направление реакций на основании мысленно представленной упругой линии балки после ее нагружения внешними усилиями (рис 8.5): при «отрыве» балки от опоры (опора А ) реакция R А имеет направление к опоре; при «вдавливании» балки в опору (опора В ) реакция R В имеет направление от опоры.
К тому времени, когда вы доберетесь до правого конца луча, диаграмма должна вернуться к нулю. Шаг 5 Хорошо отметить, что любая линия, пересекающая ось, чтобы перейти от положительной к отрицательной, следует иметь в виду при рисовании диаграммы момента, так как она становится максимальным или минимальным значением, когда наклон в нулевой точке. Шаг 6 Чтобы нарисовать диаграмму момента, вы должны сначала проверить левый конец луча, чтобы увидеть, есть ли какой-либо момент времени. Если это так, произойдет скачок от нуля до величины точечной нагрузки.

Рисунок 8.5 – К определению направлению реакций
Рассмотрим типичные случаи определения реакций для простейших видов нагрузок.
Если на балку действует интенсивностью q , как показано на рис.8.6, то при определении опорных реакций нагрузка заменяется ее равнодействующей Р , равной произведению интенсивности нагрузки q на длину участка ее действия l
Если бы не было моментального момента на диаграмму свободного тела, с которой вы начнете свою диаграмму с нуля. Шаг 7 Площадь под диаграммой сдвига - это наклон момента на диаграмме момента. Поэтому, чтобы сделать это простым, разделите диаграмму сдвига на общие фигуры и вычислите площадь каждого из них и значение, которое вы получите, могут быть построены на диаграмме момента. Вы сделаете это, перемещаясь по направлению к правой стороне луча.
Также нарисуйте диаграмму сдвига и момента для луча, как показано ниже. Схема сдвига и момента для примера 1 показана ниже. Примечание. Вы можете проверить, правильный ли ваш ответ или нет, сравнивая значения сдвига, полученные в методе разреза, с значениями сдвиговой диаграммы, если оба значения равны, то решение является правильным и безошибочным.
Примером сплошной равномерно распределенной нагрузки может служить собственный вес балки или часто расположенные нагрузки на участке ее длины.

Рисунок 8.6 – Случай равномерно распределенной нагрузки на балку
Точка приложения сплошной равномерно распределенной нагрузки q лежит посредине того участка, на который она действует; при треугольном законе действия распределенной нагрузки равнодействующая прикладывается по ее центру тяжести.
Пример 2. Определить уравнения осевой силы, силы сдвига и изгибающего момента как функции положения вдоль длины луча. Нарисуйте диаграмму сдвиговых сил и диаграмму изгибающего момента для луча ниже на рисунке. Затем определите неизвестные силы для каждого разреза, используя 3 уравнения равновесия.
Поиск реакций непрерывных лучей. Изолируйте каждый пролет луча и считайте, что каждый из них просто поддерживается, поддерживая первоначальную нагрузку по пролету и вычисленные конечные моменты. Разобьем еще один пролет в простые пучки, один из которых несет заданные нагрузки плюс другой луч, несущий концевые моменты и парные реакции. С помощью этого метода внутренняя реакция была разделена на части, которые можно суммировать, чтобы найти полную реакцию.
Размерность интенсивности нагрузки q выражается обычно в кН/м или кН/см.
Рассмотрим последовательность определения опорных реакций для случая нагрузки балки, показанной на рис.8.7:
1. На расчетной схеме балки показывается принятое направление реакций R А и R В , возникающих на опорах. Поскольку внешняя нагрузка действует в вертикальной плоскости перпендикулярно оси балки, то горизонтальная реакция на шарнирно-неподвижной опоре А отсутствует.
Задача 828 - Реакции непрерывного луча
Общее руководство В следующих задачах определите реакции и нарисуйте диаграммы сдвига. При решении проблем используйте моменты, определенные в контрольных задачах, если не указано иное. Непрерывный пучок несет равномерную нагрузку на два равных промежутка, как показано на рис.
При этом вы можете сократить решение, не выполняя все вычисления, связанные со вторым пролетом. Диаграммы лучей используются как фундаментальный способ научить инженеров базовой статической нагрузке. Балки представляют собой конструктивные элементы, способные выдерживать нагрузку благодаря его устойчивости к изгибу. Изгибная сила может быть результатом внешних нагрузок, веса или длины луча. Из-за этих нагрузок лучи испытывают изгибающий момент и момент сдвига.
2. Поскольку в данном случае неизвестных реакций две (R А и R В ), то в качестве равновесия для определения реакций принимается два уравнения
При составлении этих условий равновесия следует принять правило знаков для моментов сил, включая реакции. Обычно принимается такое привило для внешних (активных) знаков: если моменты от сил направлены по часовой стрелке, то они считаются положительными.
Балки классифицируются на основе их опор. Помимо балок, поддерживаемых фермой, лучи классифицируются в следующих группах. Просто поддерживается: балка поддерживается на концах, которые могут свободно вращаться и не имеют мгновенного сопротивления. Исправлено: луч с обеих сторон закреплен на месте.
Нависание: простой луч, проходящий за его опору на одном конце. Двойной нависание: простой луч с обоими концами, простирающимися за его опоры. Непрерывный: луч, проходящий более чем на две опоры. Консоль: Проецирующий луч фиксируется только на одном конце, а другой конец не имеет поддержки.
Тогда первое условие равновесия (8.4) приводит к уравнению относительно неизвестной реакции R В (см. рис.8.6)
![]()
![]()
Реакция получалась положительной, следовательно ее направление принято правильным.
Ниже мы проанализируем некоторые классические примеры загрузки этих категорий лучей. Простой луч имеет две опоры на каждом конце. Эти опоры или реакции не фиксированы, поэтому они могут свободно перемещаться. Это влияет на то, как нагрузки будут реагировать на опоры с точки зрения сдвига и момента изгиба. Если бы они были исправлены, силы сдвига и момента реагировали бы по-разному. Первый случай - сосредоточенная нагрузка, которая воздействует на луч в его центре. Величина силы при каждой реакции равна нагрузке в центре.
Для случая сосредоточенной нагрузки в центре напряжение сдвига имеет то же значение, что и сила реакции. Один создает диаграмму сдвига, анализируя силы, действующие на луч от одной стороны к другой. Если мы начнем с левой стороны, силы реакции начнут подниматься на луч. Это приводит к тому, что диаграмма сдвига возрастает до одного и того же значения и не пересекается, пока не достигнет центральной нагрузки. Затем значение сдвига направлено на то же значение, что и центральная нагрузка, и продолжается поперек без уклона до тех пор, пока он не достигнет второй реакционной нагрузки на другом конце луча.
Аналогично используем второе условие равновесия (8.4), приводящее к уравнению относительно второй реакции R А :
![]()
![]()
Снова реакция оказалась положительной, следовательно ее первоначально направление на расчетной схеме выбрано правильно.
Момент определяется аналогичным образом. Наклон диаграммы момента на интервале 0 равен значению сдвига. Изменение момента равно площади под сдвиговой диаграммой. В этом случае максимальный момент определяется следующим уравнением. Значения реакции будут определяться. Используя приведенные выше уравнения для реакционных нагрузок, вы можете изменить предыдущие формулы по мере необходимости.

Другой загрузочный футляр представляет собой единую нагрузку. Нагрузка равномерно распределена по длине луча. Распределенная нагрузка определяется количественно как нагрузка на расстояние, а также может быть приравнена к концентрированной нагрузке в определенной точке вдоль стержня. Величина силы равна площади под кривой распределенной нагрузки, а местоположение находится в центре массы распределенной нагрузки. Для этого случая сила при реакциях, которая также является максимальной поперечной силой, выражается.
3. Правильность определения величин реакций проверяем из использования еще одного, ранее не использованного, условия равновесия
При этом проекции сил, совпадающих с направлением оси у , считаются положительными, а направленных в обратную сторону – отрицательными.
Тогда на основании использования условия (8.5) имеем:
Здесь сдвиговая диаграмма и диаграмма момента слегка меняются. В первом случае диаграмма сдвига проходит прямо до тех пор, пока она не столкнется с нагрузкой и не сдвинется в противоположную сторону. Сдвиг во втором случае является непрерывным отрицательным наклоном. Чтобы найти поперечную силу в любой точке, используйте уравнение.
Максимальный момент может быть определен. 
Для фиксированного пучка разница будет видна на диаграмме момента. Силы реакции такие же, как и в простой пучке. Диаграмма сдвига также будет вести себя так, как было обнаружено в первом случае простого пучка. Однако теперь, когда концы зафиксированы, момент в опорах будет достигнут по-разному. Момент в центре и на концах может быть выражен с использованием того же уравнения.
![]()
Полученное тождество (0=0) свидетельствует о правильности определения величин реакций в расчете изгиба балки.
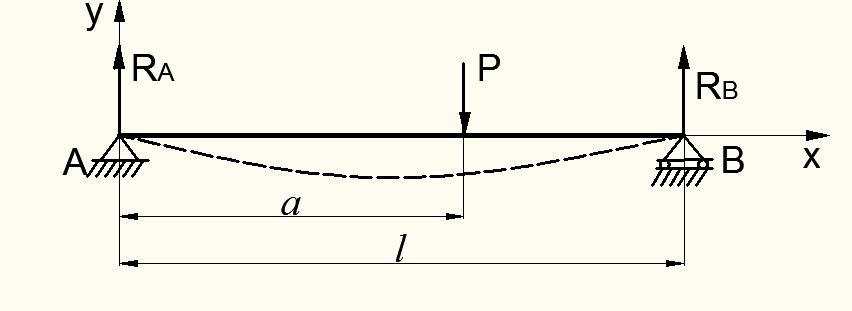
Рассмотрим другой типичный случай нагрузки в виде внецентренно расположенной сосредоточенной силы Р по длине балки l (рис.8.7).

Нависающий луч имеет первую опору на конце луча, а вторая опора расположена вдоль пучка к центру. В этом конкретном примере часть пучка, которая проходит вторую опору, не испытывает сдвига или изгиба. Визуальное изображение сдвига и изгиба похоже на простой пучок. Однако, поскольку приведенный выше пример не имеет центральной нагрузки, расчеты сдвига будут разными для каждой опоры.
Максимальный момент рассчитывается по следующему уравнению. 
Двойной нависающий луч является тем же понятием, что и одиночный, за исключением обеих опор, расположенных вдоль и внутри длины луча. В этом случае нагрузка поперек пучка является равномерной нагрузкой и более эффективно воздействует на диаграммы сдвига и изгиба. Слева направо первое значение сдвига определяется расстоянием первой опоры до конца, умноженным на равномерную нагрузку.
Рисунок 8.7 – Случай нагрузки балки сосредоточенной силой
1. Покажем на расчетной схеме реакции R А и R В . Они направлены, как было указано выше, навстречу нагрузке.
2. Реакции определим из условий равновесия:
Реакции получились положительными, следовательно, их первоначальное направление на расчетной схеме выбрано верно.
Заметим заодно, что реакция на опоре В оказалась больше, чем реакция на опоре А : R В ˃R А . Это следует из того, что сила Р находится ближе к опоре В , а значит и нагружает ее больше.
3. Проверка:
Полученное тождество свидетельствует о правильности определения реакции.
Рассмотрим еще один случай нагрузки балки в пролете внешним сосредоточенным моментом (рис. 8.8), что имеет место в практических расчетах изгиба.
| 𝔐 |

Рисунок 8.8 – Случай нагружения балки сосредоточенным моментом
1. Покажем на расчетной схеме предполагаемое направление реакций (вначале мы не знаем, правильно ли приняты такие направления).
2. Реакции определяем из уравнений равновесия:
Реакция получилась положительной, следовательно, ее первоначальное положение выбрано верно.
Реакция оказалась отрицательной, а это означает, что ее направление выбрано неправильно. Поэтому на расчетной схеме зачеркиваем первоначально (ошибочно) принятое направление R А и показываем обратное (истинное) направление (см.ри.8.8). В дальнейших расчетах считаем реакцию R А с правильным направлением положительной.
3. Проверка:
Использованное уравнение равновесия для балки выполняется, а это означает правильность определения реакций и их направления.
Если балка при поперечном изгибе имеет такие опоры, что общее число реакций, возникающих на опорах, не превышают двух, то реакции всегда могут быть определены из двух уравнений равновесия типа (8.2). Такие балки, реакции которых определяются из этих уравнений статики, называются статически определимыми балками. Эти балки могут быть таких простейших видов (рис. 8.9):
Рисунок 8.9 – Статически определимые балки
1) балка с одним жестко защемленным и другим свободным концом, иначе консоль (рис.8.9, а ); 2) шарнирно-опертые балки (рис.8.9, б и 8.9, в ).
Балки, у которых общее число реакций опор больше числа уравнений равновесия, называются статически неопределимыми (расчет их изгиба будет рассмотрен в п. 8.10). Для таких балок реакции опор определяются из совместного решения уравнений статики и условий совместимости деформаций.
Рассмотренный в § 2.7 свободный брус был нагружен заданными нагрузками (силами и моментами), находящимися в равновесии (см. рис. 3.7). Обычно заданные нагрузки не бывают взаимно уравновешенными; неподвижность конструкции под действием этих нагрузок обеспечивается благодаря наличию опор, соединяющих ее с основанием. В опорах возникают реакции, которые вместе с заданными нагрузками представляют уравновешенную систему внешних сил, действующих на конструкцию.
Как известно из курса теоретической механики, любое тело обладает в плоскости тремя степенями свободы. Поэтому для обеспечения геометрической неизменяемости системы (бруса) необходимо наложить на нее (в плоскости) три связи.
Рассмотрим различные типы опор плоских систем.
1. Защемление, или заделка (рис. 4.7, а). Защемленный (или заделанный) конец бруса не может ни смещаться поступательно, ни поворачиваться. Следовательно, число степеней свободы бруса с защемленным концом равно нулю. В опоре могут возникать: вертикальная реакция (сила R - рис. 4.7, а), препятствующая вертикальному смещению конца бруса; горизонтальная реакция (сила Н), исключающая возможность его горизонтального смещения и реактивный момент препятствующий повороту. Таким образом, закрепление бруса с помощью заделки накладывает на него три связи и обеспечивает его неподвижность.
2. Шарнирно неподвижная опора (рис. 4.7, б). Поперечное сечение бруса, проходящее через шарнирно неподвижную опору, не может смещаться поступательно. В опоре возникает реактивная сила, проходящая через центр шарнира. Ее составляющими являются вертикальная сила R, препятствующая вертикальному смещению, и горизонтальная сила Н, исключающая горизонтальное смещение закрепленного сечения бруса. Опора не препятствует повороту бруса относительно центра шарнира, и, следовательно, брус, закрепленный при помощи одной такой опоры, имеет одну степень свободы. Закрепление бруса с помощью шарнирно неподвижной опоры, накладывает на него две связи.
3. Шарнирно подвижная опора (рис. 4.7, в). Поперечное сечение бруса, проходящее через шарнирно подвижную опору, может смещаться параллельно опорной плоскости и поворачиваться, но оно не может смещаться перпендикулярно к опорной плоскости. В опоре возникает только одна реакция в виде силы R, перпендикулярной к опорной плоскости. Закрепление бруса с помощью такой опоры накладывает на него одну связь.
Рассмотренные типы опор принято также изображать с помощью стерженьков.
Шарнирно подвижную опору изображают в виде стерженька, имеющего по концам шарниры (рис. 5.7, а). Нижний шарнир неподвижен, а верхний может смещаться лишь по прямой линии, перпендикулярной к оси стерженька.

Это соответствует тем условиям закрепления, которые обеспечивает шарнирно подвижная опора (см. рис. 4.7, в). Опорная реакция действует только вдоль оси стерженька. Собственные деформации его при расчетах не учитываются, т. е. стерженек считается бесконечно жестким.
Шарнирно неподвижную опору изображают с помощью двух стерженьков с шарнирами по концам (рис. 5.7, б). Верхний шарнир является общим для обоих стерженьков. Направления стерженьков могут быть произвольными. Они, однако, не должны быть расположены на одной прямой.
Заделку (защемление) можно изображать с помощью трех стерженьков с шарнирами по концам, как показано на рис. 5.7, в.
Число стерженьков в схематическом изображении опоры равно числу составляющих опорной реакции и числу связей, накладываемых этой опорой на конструкцию.
Для того чтобы брус не перемещался под нагрузкой, он должен быть геометрически неизменяемо (неподвижно) соединен с основанием, что в случае плоского действия сил, как уже отмечалось, достигается путем наложения на него трех внешних связей.

Это можно сделать с помощью одной заделки (рис. 6.7, а) или одной шарнирно неподвижной и одной шарнирно подвижной опоры (рис. 6.7, б), или с помощью трех шарнирно подвижных опор, направления реакций которых не пересекаются в одной точке (рис. 6.7, в).

Если направления трех опорных стерженьков пересекаются в одной точке О (рис. 7.7, а,б), то система является мгновенно изменяемой, так как в этом случае ни один опорный стерженек не препятствует весьма малому повороту бруса вокруг точки О; такое расположение опорных стерженьков недопустимо.
Рассмотрим геометрически неизменяемые системы, состоящие из нескольких брусьев.

На рис. 8.7, а, например, показана система из двух брусьев (АВ и ВС), на каждый из которых наложено три связи. На брус ВС одну связь накладывает опорный стерженек CD, препятствующий вертикальному смещению точки С бруса, и две связи - шарнир В, препятствующий вертикальному и горизонтальному смещению точки В бруса.
На брус АВ все три связи налагает заделка А; шарнир же В не может препятствовать ни поступательным смещениям, ни поворотам бруса АВ и, следовательно, не налагает на него связей.
На рис. 8.7, б показана геометрически неизменяемая система, состоящая из трех брусьев (АС, CD и DF). На каждый из них наложено три связи. Так, например, шарнир С налагает на брус CD две связи (так как препятствует горизонтальному и вертикальному смещениям точки С), а шарнир - одну связь (так как препятствует только вертикальному смещению точки ).
Системы, изображенные на рис. 8.7, называются многопролетными шарнирными балками.
Общее число неизвестных опорных реакций при вариантах закрепления бруса, показанных на рис. 6.7, а, б, в, равно трем. Следовательно, эти реакции можно найти при помощи трех уравнений равновесия, которые составляются для плоской системы сил. По значениям же опорных реакций и внешних нагрузок можно определить [по формулам (2.7) - (4.7)] внутренние усилия в любом поперечном сечении бруса. Поэтому брус, закрепленный путем наложения на него трех связей, является не только геометрически неизменяемым, но и статически определимым. Наложение на него большего числа связей делает брус статически неопределимым, так как в этом случае все опорные реакции нельзя определить из одних лишь уравнений равновесия.
Уравнения равновесия, составляемые для определения опорных реакций, можно представить в трех различных вариантах:
1) в виде сумм проекций сил на две произвольные не параллельные друг другу оси и суммы моментов сил относительно любой точки плоскости МО);
2) в виде суммы проекций сил на произвольную ось и двух сумм моментов относительно любых точек плоскости, не лежащих на одном перпендикуляре к указанной оси проекций
3) в виде трех сумм моментов относительно любых точек плоскости, не лежащих на одной прямой
Выбор того или иного варианта составления уравнений равновесия, а также выбор точек и направлений осей, используемых при составлении этих уравнений, производится в каждом конкретном случае с таким расчетом, чтобы по возможности не проводить совместное решение уравнений. Для проверки правильности определения опорных реакций полученные их значения рекомендуется подставить в какое-либо уравнение равновесия, не использованное ранее.
На многопролетную шарнирную балку, изображенную на рис. 8.7, а, наложено четыре внешние связи (три в сечении А и одна в сечении С), а на балку, изображенную на рис. 8.7, б, - пять внешних связей (две в сечении А и по одной в сечениях В, Е и F).
Однако если на каждый брус, составляющий многопролетную шарнирную балку, наложено по три связи, то эта балка статически определима и опорные реакции можно найти из уравнений статики.
Кроме трех уравнений равновесия всех сил, действующих на многопролетную шарнирную балку, составляются уравнения, выражающие равенство нулю моментов сил, приложенных по одну сторону от каждого шарнира (соединяющего отдельные части балки), относительно центра этого шарнира. Например, для балки, изображенной на рис. 8.7, а, кроме трех уравнений равновесия всех действующих на нее сил, составляется уравнение моментов левых (или правых) сил относительно шарнира , а для балки, изображенной на рис. 8.7,б, - относительно шарниров С и D.

Рассмотрим пример определения опорных реакций простой однопролетной балки, расчетная схема которой изображена на рис. 9.7, а. Отбросим опоры и заменим их влияние на балку опорными реакциями RA, Н и RB (рис. 9.7, б). Обычно балка с отброшенными опорами отдельно не изображается, а обозначения и направления опорных реакций указываются на расчетной схеме балки. Реакции представляют собой вертикальную и горизонтальную составляющие полной реакции шарнирно неподвижной опоры А; сила же является полной реакцией опоры В. Направления опорных реакций выбираются произвольно; если в результате расчета значение какой-либо реакции получается отрицательным, то, значит, в действительности ее направление противоположно предварительно принятому.
Найдем сначала опорную реакцию Н, составив для этого сумму проекций всех сил на горизонтальную ось х:
Для проверки найденных значений опорных реакций составим сумму проекций всех сил на ось у.
Составленное уравнение удовлетворяется, что указывает на правильность определения опорных реакций.