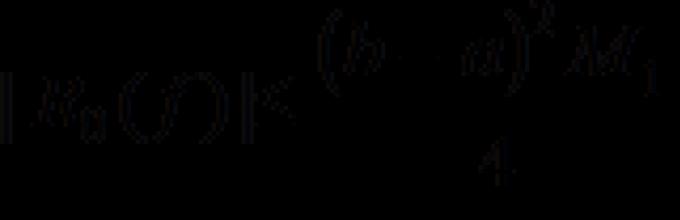Formulas atlikušā termina aprēķins:
 ,
,  .
.
Pakalpojuma uzdevums. Pakalpojums paredzēts noteikta integrāļa tiešsaistes aprēķināšanai, izmantojot taisnstūru formulu.
Instrukcija. Ievadiet integrandu f(x) , noklikšķiniet uz Atrisināt. Iegūtais risinājums tiek saglabāts Word failā. Risinājuma veidne tiek izveidota arī programmā Excel. Zemāk ir video instrukcija.
Funkciju ievadīšanas noteikumi
Piemēri≡ x^2/(1+x)
cos 2 (2x+π) ≡ (cos(2*x+pi))^2
≡ x+(x-1)^(2/3) Šī ir vienkāršākā kvadratūras formula integrāļa aprēķināšanai, kas izmanto vienu funkcijas vērtību
 (1)
(1)
kur; h = x 1 - x 0 .
Formula (1) ir taisnstūru centrālā formula. Aprēķināsim atlikumu. Izvērsīsim funkciju y=f(x) punktā ε 0 Teilora sērijā:
(2)
kur ε 1 ; x∈. Mēs integrējam (2):
 (3)
(3)
Otrajā termiņā integrands ir nepāra, un integrācijas robežas ir simetriskas attiecībā pret punktu ε 0 . Tāpēc otrais integrālis ir vienāds ar nulli. Tādējādi no (3) izriet  .
.
Tā kā integranda otrais faktors zīmi nemaina, tad ar vidējās vērtības teorēmu iegūstam  , kur. Pēc integrācijas mēs iegūstam
, kur. Pēc integrācijas mēs iegūstam  . (4)
. (4)
Salīdzinot ar trapecveida formulas atlikušo daļu, redzam, ka taisnstūra formulas kļūda ir divas reizes mazāka nekā trapecveida formulas kļūda. Šis rezultāts ir patiess, ja taisnstūru formulā ņemam funkcijas vērtību viduspunktā.
Iegūstam taisnstūru formulu un intervāla atlikušo terminu. Dots režģis x i =a+ih, i=0,1,...,n, h=x i+1 -x i. Aplūkosim režģi ε i =ε 0 +ih, i=1,2,..,n, ε 0 =a-h/2. Tad  . (5)
. (5)
Atlikušais termiņš ![]() .
.
Ģeometriski taisnstūru formulu var attēlot ar šādu attēlu: 
Ja funkcija f (x) ir dota tabulā, tad tiek izmantota vai nu taisnstūra kreisās puses formula (viendabīgam režģim) 
vai taisnstūru labās puses formula
 .
.
Šo formulu kļūda tiek novērtēta, izmantojot pirmo atvasinājumu. Intervālam kļūda ir
 ; .
; .
Pēc integrācijas mēs iegūstam .
Piemērs. Aprēķiniet integrāli n=5:
a) pēc trapecveida formulas;
b) pēc taisnstūru formulas;
c) pēc Simpsona formulas;
d) pēc Gausa formulas;
e) pēc Čebiševa formulas.
Aprēķiniet kļūdu.
Risinājums. 5 integrācijas mezgliem režģa solis būs 0,125.
Risinot izmantosim funkciju vērtību tabulu. Šeit f(x)=1/x.
| x | f(x) | ||
| x0 | 0.5 | y0 | 2 |
| x1 | 0.625 | y1 | 1.6 |
| x2 | 0.750 | y2 | 1.33 |
| x3 | 0.875 | y3 | 1.14 |
| x4 | 1.0 | y4 | 1 |
I=h/2×;
I=(0,125/2)×= 0.696;
R = [-(b-a)/12] × h × y¢¢ (x);
f¢¢(x)=2/(x3).
Funkcijas otrā atvasinājuma maksimālā vērtība intervālā ir 16: max (f¢¢(x)), xн=2/(0.5 3)=16, tāpēc
R = [-(1-0,5)/12] × 0,125 × 16 = - 0.0833;
b) taisnstūru formula:
kreisajai formulai I=h×(y0+y1+y2+y3);
I=0,125×(2+1,6+1,33+1,14)= 0.759;
R=[(b-a)/6] × h 2 × y¢¢ (x);
R = [(1-0,5)/6] × 0,125 2 × 16 = 0.02;
c) Simpsona formula:
I=(2h/6)×(y0+y4+4×(y1+y3)+2×y2);
I=(2×0,125)/6×(2+1+4×(1,6+1,14)+2×1,33)= 0.693;
R = [-(b-a)/180] × h 4 × y (4) (x);
f(4)(x)=24/(x5)=768;
R = [-(1-0,5)/180] × (0,125) 4 × 768 = - 5.2 e-4;
d) Gausa formula:
I=(b-a)/2×;
x i =(b+a)/2+t i (b-a)/2
(A i , t i - tabulas vērtības).
| t (n=5) | A (n=5) | ||||||
| x1 | 0.9765 | y1 | 1.02 | t1 | 0.90617985 | A 1 | 0.23692688 |
| x2 | 0.8846 | y2 | 1.13 | t2 | 0.53846931 | A2 | 0.47862868 |
| x3 | 0.75 | y3 | 1.33 | t3 | 0 | A 3 | 0.56888889 |
| x4 | 0.61 | y4 | 1.625 | t4 | -0.53846931 | A4 | 0.47862868 |
| x5 | 0.52 | y5 | 1.91 | t5 | -0.90617985 | A5 | 0.23692688 |
e) Čebiševa formula:
I=[(b-a)/n] ×S f(x i), i=1..n,
x i =(b+a)/2+[ t i (b-a)]/2 - nepieciešamā integrācijas intervāla samazināšana līdz intervālam [-1;1].
Ja n=5
| t1 | 0.832498 |
| t2 | 0.374541 |
| t3 | 0 |
| t4 | -0.374541 |
| t5 | -0.832498 |
| x1 | 0,958 | f(x1) | 1,043 |
| x2 | 0,844 | f(x2) | 1,185 |
| x3 | 0,75 | f(x3) | 1,333 |
| x4 | 0,656 | f(x4) | 1,524 |
| x5 | 0,542 | f(x5) | 1,845 |
I=(1-0,5)/5×6,927=0,6927.
Taisnstūris ir četrstūris, kurā katrs stūris ir taisns leņķis.
Pierādījums
Īpašība ir izskaidrojama ar paralelograma 3. pazīmes darbību (t.i., \angle A = \angle C , \angle B = \angle D )
2. Pretējās puses ir vienādas.
AB = CD,\enspace BC = AD

3. Pretējās puses ir paralēlas.
AB \parallel CD,\enspace BC \parallel AD
4. Blakus esošās malas ir perpendikulāras viena otrai.
AB \perp BC,\enspace BC \perp CD,\enspace CD \perp AD,\enspace AD \perp AB

5. Taisnstūra diagonāles ir vienādas.
AC=BD

Pierādījums
Saskaņā ar īpašums 1 taisnstūris ir paralelograms, kas nozīmē AB = CD.

Tāpēc \trijstūris ABD = \trijstūris DCA gar divām kājām (AB = CD un AD - savienojums).
Ja abi skaitļi - ABC un DCA ir identiski, tad arī to hipotenūzas BD un AC ir identiskas.
Tātad AC = BD.
Tikai visu figūru taisnstūrim (tikai no paralelogramiem!) ir vienādas diagonāles.
Pierādīsim arī to.

ABCD ir paralelograms \Rightarrow AB = CD , AC = BD pēc nosacījuma. \Labā bultiņa \trijstūris ABD = \trijstūris DCA jau no trim pusēm.
Izrādās, ka \angle A = \angle D (kā paralelograma stūri). Un \angle A = \angle C , \angle B = \angle D .
Mēs to secinām \leņķis A = \leņķis B = \leņķis C = \leņķis D. Tie visi ir 90^(\circ) . Kopā ir 360^(\circ) .
Pierādīts!
6. Kvadrātveida diagonāle ir vienāda ar summu tā divu blakus malu kvadrāti.
Šī īpašība ir spēkā, pamatojoties uz Pitagora teorēmu.
AC^2=AD^2+CD^2
7. Diagonāle sadala taisnstūri divos identiskos taisnleņķa trīsstūros.
\trijstūris ABC = \trijstūris ACD, \enspace \trijstūris ABD = \trijstūris BCD

8. Diagonāļu krustpunkts sadala tās uz pusēm.
AO=BO=CO=DO
.png)
9. Diagonāļu krustpunkts ir taisnstūra un ierobežotā apļa centrs.

10. Visu leņķu summa ir 360 grādi.
\angle ABC + \angle BCD + \angle CDA + \angle DAB = 360^(\circ)
11. Visi taisnstūra stūri ir taisni.
\angle ABC = \angle BCD = \angle CDA = \angle DAB = 90^(\circ)

12. Ap taisnstūri apzīmētā riņķa diametrs ir vienāds ar taisnstūra diagonāli.

13. Apli vienmēr var aprakstīt ap taisnstūri.
Šī īpašība ir derīga, jo taisnstūra pretējo stūru summa ir 180^(\circ)
\angle ABC = \angle CDA = 180^(\circ),\enspace \angle BCD = \angle DAB = 180^(\circ)
14. Taisnstūrī var būt ierakstīts aplis un tikai viens, ja tam ir vienādi malu garumi (tas ir kvadrāts).
Vispār kreisā taisnstūra formula segmentā sekojoši (21) :
Šajā formulā x 0 =a, x n =b, jo jebkurš integrālis kopumā izskatās šādi: (skatiet formulu 18 ).
h var aprēķināt, izmantojot formulu 19 .
y 0 ,y 1 ,...,y n-1 x 0 , x 1 ,...,x n-1 (x i =x i-1 +h).
Taisnstūra taisnstūru formula.
Vispār taisnstūra formula segmentā sekojoši (22) :
Šajā formulā x 0 =a, x n =b(sk. kreiso taisnstūru formulu).
h var aprēķināt, izmantojot to pašu formulu kā kreiso taisnstūru formulā.
y 1 ,y 2 ,...,y n ir atbilstošās funkcijas f(x) vērtības punktos x 1 , x 2 ,...,x n (x i =x i-1 +h).
Vidēja taisnstūra formula.
Vispār vidējā taisnstūra formula segmentā sekojoši (23) :
Kur x i =x i-1 +h.
Šajā formulā, tāpat kā iepriekšējās, ir nepieciešams h reizināt funkcijas f (x) vērtību summu, bet ne tikai aizstājot atbilstošās vērtības x 0 ,x 1 ,...,x n-1 funkcijā f(x) un pievienojot katrai no šīm vērtībām h/2(x 0 +h/2, x 1 +h/2,..., x n-1 +h/2) un tikai pēc tam tos aizstājot ar doto funkciju.
h var aprēķināt, izmantojot to pašu formulu kā kreiso taisnstūru formulā." [ 6 ]
Praksē šīs metodes tiek īstenotas šādi:
Mathcad ;
Excel .
Mathcad ;
Excel .
Lai aprēķinātu integrāli, izmantojot Excel vidējo taisnstūru formulu, jāveic šādas darbības:
Turpiniet darbu tajā pašā dokumentā, kā aprēķinot integrāli, izmantojot kreisā un labā taisnstūra formulas.
Ievadiet tekstu xi+h/2 šūnā E6 un f(xi+h/2) šūnā F6.
Ievadiet formulu =B7+$B$4/2 šūnā E7, kopējiet šo formulu, velkot uz šūnu diapazonu E8:E16
Šūnā F7 ievadiet formulu =ROOT(E7^4-E7^3+8), kopējiet šo formulu, velkot uz šūnu diapazonu F8:F16.
Šūnā F18 ievadiet formulu =SUM(F7:F16).
Šūnā F19 ievadiet formulu =B4*F18.
Ievadiet vidējo vērtību tekstu šūnā F20.
Rezultātā mēs iegūstam sekojošo:

Atbilde: dotā integrāļa vērtība ir 13.40797.
Pamatojoties uz iegūtajiem rezultātiem, var secināt, ka vidējo taisnstūru formula ir precīzāka nekā labā un kreisā taisnstūra formulas.
1. Montekarlo metode
"Montekarlo metodes galvenā ideja ir izlases veida testu atkārtota atkārtošana. Montekarlo metodes raksturīga iezīme ir nejaušu skaitļu (dažu skaitlisko vērtību) izmantošana. izlases lielums). Šādus skaitļus var iegūt, izmantojot nejaušo skaitļu ģeneratorus. Piemēram, Turbo Pascal programmēšanas valodai ir standarta funkcija nejauši, kuru vērtības ir nejauši skaitļi, kas vienmērīgi sadalīti pa intervālu . Sacītais nozīmē, ka, ja norādīto segmentu sadala noteiktā skaitā vienādu intervālu un aprēķina nejaušās funkcijas vērtību liels skaitlis reizes, tad katrā intervālā iekritīs aptuveni vienāds nejaušu skaitļu skaits. Baseina programmēšanas valodā līdzīgs sensors ir rnd funkcija. Izklājlapā MS Excel funkcija RAND atgriež vienmērīgi sadalītu nejaušu skaitli, kas ir lielāks vai vienāds ar 0 un mazāks par 1 (pārrēķinot izmaiņas)" [ 7 ].
Lai to aprēķinātu, jāizmanto formula () :
Kur (i=1, 2, …, n) ir nejauši skaitļi, kas atrodas intervālā .
Lai iegūtu šādus skaitļus, pamatojoties uz nejaušu skaitļu secību x i, kas vienmērīgi sadalīti intervālā , pietiek ar transformāciju x i =a+(b-a)x i .
Praksē šī metode tiek īstenota šādi:
Lai programmā Excel aprēķinātu integrāli ar Montekarlo metodi, jāveic šādas darbības:
Šūnā B1 ievadiet tekstu n=.
Šūnā B2 ievadiet tekstu a=.
Šūnā B3 ievadiet tekstu b=.
Ievadiet skaitli 10 šūnā C1.
Ievadiet skaitli 0 šūnā C2.
Šūnā C3 ievadiet numuru 3.2.
Šūnā A5 ievadiet I, B5 - xi, C5 - f (xi).
Šūnas A6:A15 aizpilda ar skaitļiem 1,2,3, ..., 10 - jo n=10.
Šūnā B6 ievadiet formulu =RAND()*3.2 (skaitļi tiek ģenerēti diapazonā no 0 līdz 3,2), kopējiet šo formulu, ievelkot šūnu diapazonā B7:B15.
Ievadiet formulu =ROOT(B6^4-B6^3+8) šūnā C6, kopējiet šo formulu, velkot to šūnu diapazonā C7:C15.
Šūnā B16 ievadiet tekstu "summa", B17 šūnā "(b-a)/n" un B18 šūnā "I=".
Šūnā C16 ievadiet formulu =SUM(C6:C15).
Šūnā C17 ievadiet formulu =(C3-C2)/C1.
Šūnā C18 ievadiet formulu =C16*C17.
Rezultātā mēs iegūstam:

Atbilde: dotā integrāļa vērtība ir 13.12416.
Definīcija.
Taisnstūris Tas ir četrstūris, kura divas pretējās malas ir vienādas un visi četri leņķi ir vienādi.Taisnstūri viens no otra atšķiras tikai ar garās malas attiecību pret īso malu, bet visi četri ir taisni, tas ir, katrs 90 grādu leņķī.
Taisnstūra garo malu sauc taisnstūra garums, un īsais taisnstūra platums.
Taisnstūra malas ir arī tā augstums.
Taisnstūra pamatīpašības
Taisnstūris var būt paralelograms, kvadrāts vai rombs.
1. Taisnstūra pretējām malām ir vienāds garums, tas ir, tās ir vienādas:
AB = CD, BC = AD
2. Taisnstūra pretējās malas ir paralēlas:
3. Taisnstūra blakus esošās malas vienmēr ir perpendikulāras:
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
4. Visi četri taisnstūra stūri ir taisni:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
5. Taisnstūra leņķu summa ir 360 grādi:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
6. Taisnstūra diagonālēm ir vienāds garums:
7. Taisnstūra diagonāles kvadrātu summa ir vienāda ar malu kvadrātu summu:
2d2 = 2a2 + 2b2
8. Katra taisnstūra diagonāle sadala taisnstūri divās identiskās figūrās, proti, taisnstūra trīsstūros.
9. Taisnstūra diagonāles krustojas un tiek dalītas uz pusēm krustpunktā:
| AO=BO=CO=DO= | d | ||
| 2 |
10. Diagonāļu krustpunktu sauc par taisnstūra centru, un tas ir arī ierobežotā apļa centrs.
11. Taisnstūra diagonāle ir ierobežotā apļa diametrs
12. Apli vienmēr var aprakstīt ap taisnstūri, jo pretējo leņķu summa ir 180 grādi:
∠ABC = ∠CDA = 180° ∠BCD = ∠DAB = 180°
13. Apli nevar ierakstīt taisnstūrī, kura garums nav vienāds ar tā platumu, jo pretējo malu summas nav vienādas viena ar otru (apli var ierakstīt tikai speciālā taisnstūra gadījumā - kvadrātā).
Taisnstūra malas
Definīcija.
Taisnstūra garums sauciet garākā tā malu pāra garumu. Taisnstūra platums nosauciet tā sānu īsākā pāra garumu.Formulas taisnstūra malu garumu noteikšanai
1. Formula taisnstūra malai (taisnstūra garums un platums) diagonāles izteiksmē un otrās malas izteiksmē:
a = √ d 2 - b 2
b = √ d 2 - a 2
2. Formula taisnstūra malai (taisnstūra garums un platums) laukuma izteiksmē un otrās malas izteiksmē:
| b = dcos | β |
| 2 |
Taisnstūra diagonāle
Definīcija.
Diagonāls taisnstūris Tiek izsaukts jebkurš segments, kas savieno divas taisnstūra pretējo stūru virsotnes.Formulas taisnstūra diagonāles garuma noteikšanai
1. Formula taisnstūra diagonālei taisnstūra divu malu izteiksmē (izmantojot Pitagora teorēmu):
d = √ a 2 + b 2
2. Formula taisnstūra diagonālei laukuma un jebkuras malas izteiksmē:
4. Formula taisnstūra diagonālei attiecībā uz ierobežotā apļa rādiusu:
d=2R
5. Taisnstūra diagonāles formula, kas izteikta ierobežotā apļa diametra izteiksmē:
d = D o
6. Taisnstūra diagonāles formula, kas izteikta diagonālei piegulošā leņķa sinusa izteiksmē un šim leņķim pretējās malas garumā:
8. Taisnstūra diagonāles formula akūtā leņķa sinusa izteiksmē starp diagonālēm un taisnstūra laukumu
d = √2S: sinβ
Taisnstūra perimetrs
Definīcija.
Taisnstūra perimetrs ir taisnstūra visu malu garumu summa.Formulas taisnstūra perimetra garuma noteikšanai
1. Formula taisnstūra perimetram abās taisnstūra malās:
P = 2a + 2b
P = 2(a+b)
2. Formula taisnstūra perimetra laukumam un jebkurai malai:
| P= | 2S + 2a 2 | = | 2S + 2b 2 |
| a | b |
3. Formula taisnstūra perimetram diagonāles un jebkuras malas izteiksmē:
P = 2(a + √ d 2 - a 2) = 2(b + √ d 2 - b 2)
4. Taisnstūra perimetra formula ierobežotā apļa un jebkuras malas rādiusa izteiksmē:
P = 2(a + √4R 2 - a 2) = 2(b + √4R 2 - b 2)
5. Taisnstūra perimetra formula, kas izteikta ierobežotā apļa un jebkuras malas diametra izteiksmē:
P = 2(a + √D o 2 - a 2) = 2(b + √D o 2 - b 2)
Taisnstūra laukums
Definīcija.
Taisnstūra laukums sauc par telpu, ko ierobežo taisnstūra malas, tas ir, taisnstūra perimetrā.Formulas taisnstūra laukuma noteikšanai
1. Taisnstūra laukuma divu malu formula:
S = a b
2. Formula taisnstūra laukumam caur perimetru un jebkuru malu:
5. Taisnstūra laukuma formula ierobežotā apļa un jebkuras malas rādiusa izteiksmē:
S = a √4R 2 - a 2= b √4R 2 - b 2
6. Formula taisnstūra laukumam, ņemot vērā ierobežotā apļa un jebkuras malas diametru:
S \u003d a √ D o 2 - a 2= b √ D o 2 - b 2
Aplis, kas norobežots ap taisnstūri
Definīcija.
Aplis, kas apvilkts ap taisnstūri Par apli sauc apli, kas iet caur četrām taisnstūra virsotnēm, kura centrs atrodas taisnstūra diagonāļu krustpunktā.Formulas ap taisnstūri norobežota riņķa rādiusa noteikšanai
1. Formula apļa rādiusam, kas apvilkts ap taisnstūri caur divām malām:
Viens no matemātikas pamatjēdzieniem ir taisnstūra perimetrs. Par šo tēmu ir daudz problēmu, kuru risināšanā nevar iztikt bez perimetra formulas un prasmēm to aprēķināt.
Pamatjēdzieni
Taisnstūris ir četrstūris, kurā visi leņķi ir taisni un pretējās malas ir pa pāriem vienādas un paralēlas. Mūsu dzīvē daudzas figūras ir taisnstūra formā, piemēram, galda virsma, piezīmju grāmatiņa utt.
Apsveriet piemēru: gar zemes robežām jānovieto žogs. Lai uzzinātu katras malas garumu, tie ir jāizmēra.

Rīsi. viens. Zemes gabals taisnstūra forma.
Zemes gabalam ir malas ar garumu 2 m, 4 m, 2 m, 4 m. Tāpēc, lai uzzinātu kopējo žoga garumu, jāsaskaita visu malu garumi:
2+2+4+4= 2 2+4 2 =(2+4) 2 =12 m.
Tieši šo vērtību parasti sauc par perimetru. Tādējādi, lai atrastu perimetru, jums jāpievieno visas figūras malas. Burts P tiek izmantots, lai apzīmētu perimetru.
Lai aprēķinātu taisnstūra figūras perimetru, jums tas nav jāsadala taisnstūros, jums ir jāizmēra tikai visas šīs figūras malas ar lineālu (mērlenti) un jāatrod to summa.
Taisnstūra perimetru mēra mm, cm, m, km un tā tālāk. Nepieciešamības gadījumā uzdevumā iekļautie dati tiek pārvērsti tajā pašā mērījumu sistēmā.
Taisnstūra perimetru mēra dažādās mērvienībās: mm, cm, m, km utt. Ja nepieciešams, uzdevuma dati tiek pārvērsti vienā mērījumu sistēmā.
Formulas perimetra formula
Ja ņemam vērā to, ka taisnstūra pretējās malas ir vienādas, tad varam iegūt taisnstūra perimetra formulu:
$P = (a+b) * 2$, kur a, b ir figūras malas.

Rīsi. 2. Taisnstūris ar apzīmētām pretējām malām.
Ir vēl viens veids, kā atrast perimetru. Ja uzdevumam ir dota tikai viena figūras puse un laukums, varat izmantot, lai izteiktu otru pusi caur laukumu. Tad formula izskatīsies šādi:
$P = ((2S + 2a2)\over(a))$, kur S ir taisnstūra laukums.
Rīsi. 3. Taisnstūris ar malām a, b.
Exercise : Aprēķiniet taisnstūra perimetru, ja tā malas ir 4 cm un 6 cm.
Risinājums:
Mēs izmantojam formulu $P = (a+b)*2$
$P = (4+6)*2=20 cm$
Tādējādi figūras perimetrs ir $ P = 20 cm $.
Tā kā perimetrs ir visu figūras malu summa, pusperimetrs ir tikai viena garuma un platuma summa. Reiziniet pusperimetru ar 2, lai iegūtu perimetru.
Platība un perimetrs ir divi pamatjēdzieni jebkuras figūras mērīšanai. Tos nevajadzētu sajaukt, lai gan tie ir saistīti. Ja palielināsit vai samazināsiet laukumu, tad attiecīgi palielināsies vai samazināsies tā perimetrs.
Ko mēs esam iemācījušies?
Mēs esam iemācījušies atrast taisnstūra perimetru. Un arī iepazinās ar tā aprēķināšanas formulu. Ar šo tēmu var saskarties ne tikai matemātikas uzdevumu risināšanā, bet arī dzīvē.
Tēmu viktorīna
Raksta vērtējums
Vidējais vērtējums: 4.5. Kopējais saņemto vērtējumu skaits: 365.