Gravitace a hmotnost
Podle zákona univerzální gravitace zažívají všechna tělesa na Zemi sílu její přitažlivosti.
Gravitační síla tělesa je mírou jeho přitažlivosti k Zemi (s přihlédnutím k vlivu rotace Země):
G = tG;[ G] = ML T-2.
Sipa gravitace závisí na hmotnosti Země a jí přitahovaného tělesa a také na vzdálenosti mezi nimi. Vzdálenost od středu Země k jejímu povrchu je menší na pólu (6357 km) a větší na rovníku (6378 km), takže gravitační síla na rovníku je o 0,2 % menší než na pólech.
Protože se Země otáčí kolem své osy, tělesa na jejím povrchu pociťují odstředivou sílu setrvačnosti (fiktivní) v neinerciální (rotující) vztažné soustavě. Největší je na rovníku a snižuje tam gravitační sílu o dalších 0,3 % (oproti poloze na pólech). Proto je gravitační síla rovna geometrickému součtu gravitačních (gravitačních) a odstředivých (inerciálních).
Gravitační síly působí na každý článek a na celé lidské tělo jako vnější síly způsobené přitažlivostí a rotací Země. Na jeho těžiště působí stejně působící rovnoběžné gravitační síly tělesa.
Když tělo spočívá na podpěře (nebo je zavěšeno), gravitační síla působící na tělo jej přitlačí k podpěře (nebo jej zvedne ze zavěšení). Toto působení těla na podpěru (spodní nebo horní) se měří hmotností těla . Tělesná hmotnost (statická) je mírou dopadu těla v klidu na podpěru (nebo závěs), která zabraňuje jeho pádu. To znamená, že gravitační síla a hmotnost tělesa nejsou stejné síly. Váha celého těla člověka nepůsobí na něj samotného, ale na jeho podporu (gravitace je vzdálená síla, váha je kontaktní síla). V letové fázi při běhu není žádná váha, jedná se o stav beztíže.
Když hlava působí na krční obratle, dochází k interakci hlavy a páteře. Hmotnost hlavy vzhledem k celému tělu člověka je tedy vnitřní silou, zatímco ve vztahu k páteři je vnější silou. Hmotnost například činky, kterou člověk drží, je pro něj samozřejmě vnější silou.
Když se těleso pohybuje se zrychlením nasměrovaným podél vertikály, vzniká vertikální síla setrvačnosti. Je směrován v opačném směru, než je zrychlení. Jestliže síla setrvačnosti směřuje dolů, pak je přidána ke statické hmotnosti; tlaková síla na podpěru se zvyšuje. Jestliže síla setrvačnosti směřuje nahoru, pak se odečte od statické hmotnosti; tlaková síla na podpěru klesá. V obou případech se změněná hmotnost nazývá dynamická, je víceméně než statická. Dynamická váha tyče v rukou sportovce na něj působí zvenčí (vnější síla). Dynamická váha trupu při vyskočení působí na nohy uvnitř těla ( vnitřní síla vzhledem k celému tělu a vnější - vzhledem k nohám).
Podporujte reakční síly
Působení tělesné hmotnosti na podpěru se setkává s protiakci, která se nazývá podpůrná reakce (nebo podpůrná reakce).
Podpora reakce- je to míra protipůsobení podpěry vůči působení těla, které je s ní v kontaktu (v klidu nebo v pohybu). Je rovna síle těla působící na podpěru, nasměrované dovnitř opačná strana a připojen k tomuto tělu.
Obvykle člověk, který je na vodorovné podpěře, zažívá odpor vůči své váze. V tomto případě je podpěrná reakce, stejně jako hmotnost těla, směrována kolmo k podpěře. Toto je normální (nebo ideální) podpůrná reakce. Pokud povrch není plochý, pak je podpěrná reakce kolmá k rovině tečné k bodu otáčení.
Když je závaží statické, reakce podpory je statická; velikostí se rovná statické hmotnosti. Pokud se člověk na podpěře pohybuje se zrychlením směrem nahoru, pak se setrvačná síla přičte ke statické hmotnosti a dojde k dynamické reakci podpěry. Reakce podpory je pasivní (reaktivní) síla. Sama o sobě nemůže způsobit pozitivní zrychlení. Ale bez ní – pokud není žádná podpora, není-li se od čeho odrážet (nebo čím by se dalo přitahovat) – se člověk nemůže aktivně pohybovat.
Pokud z vodorovné podpěry netlačíte přímo nahoru, tlaková síla na podpěru nebude působit v pravém úhlu.
na její povrch. Pak také nebude reakce nosiče kolmá k povrchu, může se rozložit na nanonormální a tangenciální složky. Když jsou styčné plochy rovné, bez výstupků, hrotů atd. (asfalt, podrážka boty), pak je tečnou složkou reakce podpory třecí síla.
Tangenciální reakce může být způsobena nejen třením (jako např. mezi lyží a sněhem), ale i jinými interakcemi (např. hroty běžeckých bot zapíchnuté do stopy).
Výslednice normálové a tečné složky se nazývá obecná reakce podpory. Lidskou CM prochází pouze tehdy, když je ve volné stacionární poloze nad podpěrou (nebo pod podpěrou). Během pohybů, odpuzování nebo znehodnocování obvykle neprochází CM a tvoří vůči němu moment.
Pojďme se seznámit se zákonem, který vám umožňuje vypočítat sílu tření. Objevil jej Francouz G. Amonton a otestoval jeho krajan C. Coulomb, proto se mu říká Amonton-Coulombův zákon.
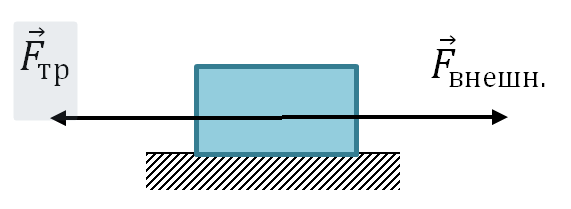
Uvažujme tělo ležící na podpěře (viz levá strana výkresu). Tělo působí na podpěru svou vahou W, která směřuje dolů. Podle třetího Newtonova zákona je podpora reaguje síla na tělo R, modul se rovná váze těla a je opačně orientovaný. Podle pravidla rovnoběžníku reakční síla R může být reprezentován jako součet normální reakční síly N kolmo k povrchu a tangenciální reakční síly T po povrchu. Tato část reakce je statická třecí síla.
Pokud podpěru umístíme vodorovně, pak bude reagovat i na tělo podle třetího Newtonova zákona (viz střední část výkresu). V tomto případě, stejně jako dříve, bude reakční síla R podpory v absolutní hodnotě rovna hmotnosti tělesa W a bude směřovat opačně. Spolu s tím bude reakční síla současně normální reakční silou a tangenciální reakční síla, třecí síla, nebude chybět. Jestliže nyní na těleso působí vnější síla F směřující po povrchu, pak opět vyvoláme vzhled tečné reakční síly. V tomto případě bude posuvná třecí síla(viz pravá strana výkresu).
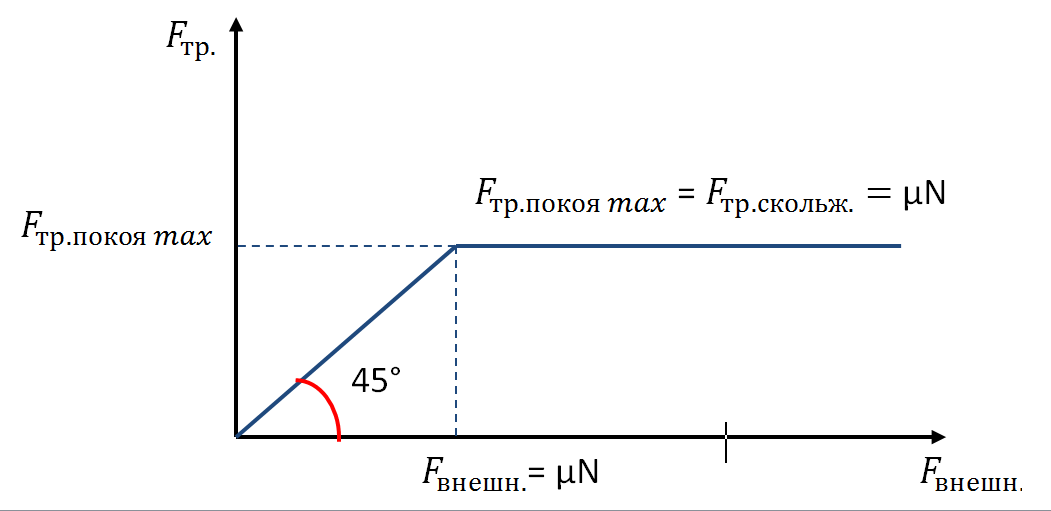
Experimenty ukazují, že když se jedno těleso pohybuje po povrchu druhého modul kluzné třecí síly je úměrný modulu normálové reakční síly podpory, vyjádřené jako Amonton-Coulombův zákon:
Jinými slovy, Amonton-Coulombův zákon udává úměrnost dvou sil: tangenciální reakce podpory (kluzná třecí síla) a reakce normální podpory (tlaková síla).
- Dříve jsme mohli měřit pouze sílu tření, nyní ...
- Amonton-Coulombův zákon se nazývá dvojitý, protože...
- Pro upřesnění nového označení ve vzorci zákona, ...
- Pokud je tělo v klidu, působí na podpěru pouze jednou silou - ...
- Protože na podporu nepůsobí pouze tělo, to znamená, že dochází k interakci, pak ...
- Použitím definice výslednice pro dvě síly "obrácené", ...
- Tangenciální složka reakční síly podpory je...
- Při vodorovné poloze podpěry, její reakční síla, jako v prvním případě, ...
- Ve druhém případě, podle pravidla pro hledání výslednice, ...
- Nákres vpravo ukazuje...
- Tangenciální složka reakce podpory na pravém výkresu je...
- Formulujte Amonton-Coulombův zákon.
- Vzorec Amonton-Coulombova zákona je skalární, protože zahrnuje ...
- Vzorec Amonton-Coulombova zákona z pohledu matematiky ...
Síly v mechanice
Na každé těleso, které se nachází v blízkosti zemského povrchu nebo leží na zemi, působí síla rovnající se součinu hmotnosti tělesa a zrychlení volného pádu:.
\vec(F)_(T)=m\vec(g)
2. Reakční síla podpory (normální reakce, elasticita podpory)
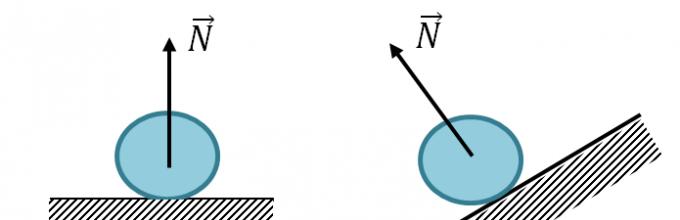
Síla působící na stranu podpěry na těleso na ní ležící. Vždy směřujte kolmo ke styčné ploše těla a podpěry.
\vec(N) - podpora reakční síly.

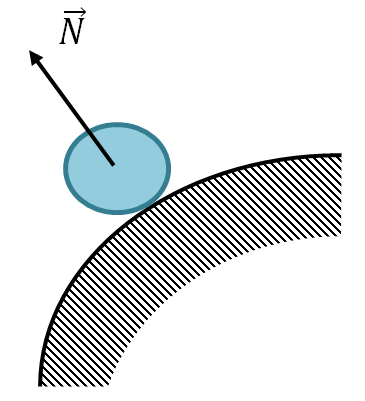
Leží-li těleso na vnitřním povrchu koule, síla \vec(N) směřuje do středu koule.

Leží-li těleso na vnějším povrchu koule, síla \vec(N) směřuje ze středu koule.
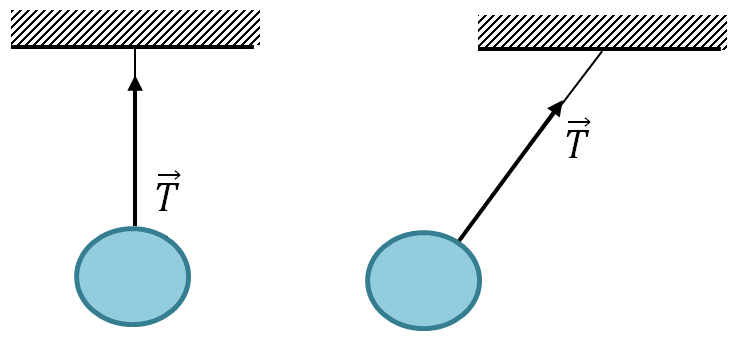
Síla působící ze strany závitu (lano, lano, lano, tyč atd.) na těleso, které visí na závitu (lano atd.). Nasměrováno podél závitu (atd.).
\vec(T)
4. Tělesná hmotnost
Definice: je síla, kterou tělo tlačí na podpěru nebo natahuje závěs.
Hmotnost tělesa je v absolutní hodnotě rovna reakční síle podpěry nebo napínací síle nitě, směřuje opačným směrem a působí na jiné těleso: buď na podpěru nebo na závit.
\vec(N) - reakční síla podpory;
\vec(P) - tělesná hmotnost.
\matrix(\vec(P)=-\vec(N)\\\mid\vec(P)\mid=\mid\vec(N)\mid)
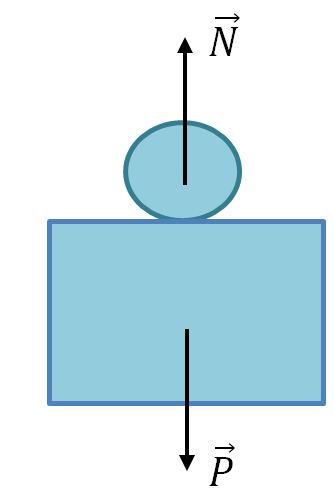
\matrix(\vec(P)=-\vec(T)\\\mid\vec(P)\mid=\mid\vec(T)\mid)
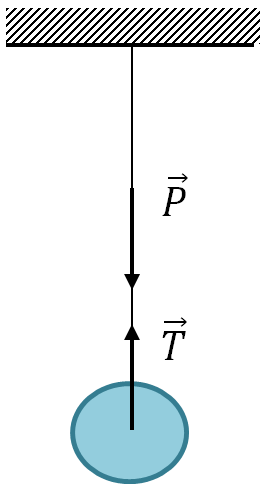
5. Síla tření
a) Kluzná třecí síla
Síla kluzného tření směřuje opačně k relativní rychlosti těles a nezávisí na ploše kontaktu mezi povrchy.
\vec(F)_(tr)
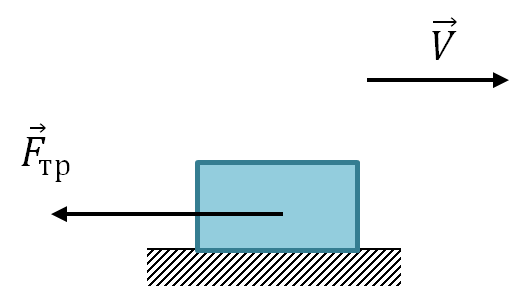
Modul třecí síly se rovná součinu součinitele kluzného tření a modulu reakční síly podpory:
\vec(F)_(tr)=\mu N
\mu - koeficient kluzného tření.
b) Valivá třecí síla
Působí na těleso, které neklouže, ale odvaluje se po určité ploše.
\vec(F)_(tr)
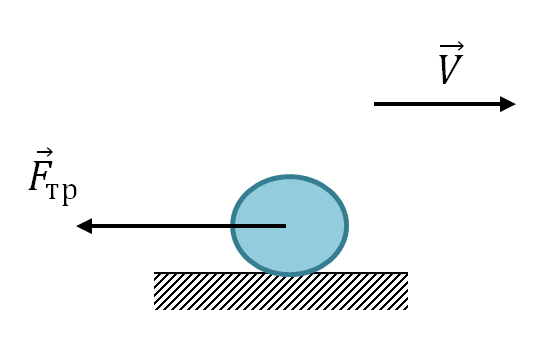
\vec(F)_(tr)=\mu _(1)N
\mu _(1) - koeficient valivého tření.
Koeficient valivého tření je mnohem menší než koeficient kluzného tření
c) Síla statického tření
Působí na těleso ležící nehybně na nějaké ploše, kterou se snažíme pohnout. Je protikladná k vnější síle a rovná se jí v absolutní hodnotě.
\vec(F)_(tr.p.)
\vec(F)_(externí) - vnější síla.
6. Schéma řešení problémů
a) Nakreslete všechny síly působící na všechna tělesa soustavy;
b) Vyberte si referenční systémy (pro každé těleso můžete mít vlastní);
c) Promítněte síly na osu;
d) Napište rovnice pro druhý Newtonův zákon v projekcích pro všechna tělesa soustavy;
e) Zapište kinematické vztahy, tedy vztahy mezi rychlostmi a zrychleními různých těles v soustavě;
f) Vyřešte výslednou soustavu rovnic.
Recenze
|
Alexandra |
|
Natalya Lvovna je skvělá učitelka, která vás dokonale připraví na zkoušku. Přišel jsem k ní ne s nulovými znalostmi, ale nelze je nazvat dobrými. Sice jsem začala studovat v lednu, ale všechna témata jsme zvládli projít v doplňkových hodinách. Každé téma bylo analyzováno a byly vyřešeny všechny typy problémů, se kterými se lze u zkoušky setkat. A skutečně, na Jednotné státní zkoušce jsem nenarazil na potíže při řešení problémů a napsal zkoušku na 94 bodů. Velmi doporučuji tohoto učitele! |
|
Ilya |
|
Začal jsem studovat s Natalyou Lvovnou v polovině ledna, hned po novoročních svátcích. Před začátkem vyučování byly zkušební zkoušky z fyziky a také příprava na zkoušku ve škole, ale výsledek byl 60-70 bodů, přičemž z předmětu jsem dostal výborné. Hodiny s Natalií Lvovnou byly plodné a zajímavé, s touto lektorkou jsem si mohl rozšířit své znalosti fyziky a také upevnit školní osnovy. Po absolvování jarních intenzivních zkoušek jsem šel na zkoušku s jistotou ve svém výsledku. Po obdržení 85 bodů jsem byl schopen vstoupit na požadovanou univerzitu s 1 mávnutím. Chci ještě jednou poděkovat tutorovi, který mi pomohl přiblížit se k mým cílům, předat singl Státní zkouška na potřebných bodech, vstoupit na vysokou školu a zahájit přípravu na budoucí povolání. |
|
Taťána |
|
Moje dcera Polina studovala na škole s „humanitární zaujatostí“. Hlavními předměty od první třídy pro ni byly cizí jazyky. Když však vyvstala otázka výběru povolání, dcera chtěla vstoupit na technickou univerzitu. To je zřejmé školní program- ne guma, a není divu, že s 8 tréninkovými hodinami cizí jazyky měla jen jednu hodinu fyziky týdně. Musel jsem naléhavě hledat řešení. Měli jsme štěstí - našli jsme skvělého lektora. |
Podporujte reakce.
Zjistili jsme, ale i bez nás se vědělo, že všechno má své hranice. Za hranicí má člověk smrt, budova má destrukci, ale každý bojuje o život. Když jsme prstem stiskli pravítko v jednom z míst, kde se pravítko opíralo o knihy, nepodařilo se nám pravítko porazit a prstem jsme cítili, jak pravítko spočinulo, ale neohnulo se ani o milimetr. Navíc čím více jsme na pravítko tlačili, tím silněji spočívalo, přičemž síla, kterou jsme na pravítko tlačili, byla srovnatelná se silou odrazu.
V reálném světě je vše velmi složité – jakákoliv látka, i velmi jednoduchá, má velmi nepochopitelnou strukturu. Některé látky se skládají z atomů spojených do krystalové mřížky, přičemž materiál může být monokrystalický nebo polykrystalický. V jiných látkách jsou atomy součástí molekul, které mohou být jednoduché i velmi složité. Ale mezi všemi těmito atomy nebo molekulami existuje přísné spojení. Všechny tyto atomy a molekuly se drží ve vzdálenosti určené přírodou, a když položíme prst na pravítko, snažíme se zmenšit vzdálenost mezi atomy nebo molekulami, ale molekuly a atomy to nechtějí a brání se, vědecky řečeno, vzniká napětí, tzn. vzdálenost mezi atomy nebo molekulami se zmenšuje, ale pokud je prst odstraněn, atomy a molekuly se vrátí na svá místa.
Když navíc vyvíjíme tlak na pravítko, dochází k deformacím nejen v hmotě pravítka, ale také v knize, v místě, kde pravítko spočívá na knize, v hmotě stolu, na kterém knihy leží, a tak dále, až do samotného jádra země. Mimochodem, pro některé látky lze pojem napětí brát doslova - tento efekt je základem pro činnost piezoelektrických prvků, ale nenecháme se rozptylovat. Když tedy položíme prst na pravítko v bodě otáčení, část energie přejde do pružné deformace, část do nepružné deformace, část do zahřívání látky, část více do zvukových vibrací a tak dále, jedním slovem proces je složitý, ale na stavební mechanice miluji to, že ve stavebnictví je vše jednoduché, protože stavební mechanika nebyla vynalezena proto, aby nám komplikovala život, ale aby nám zjednodušila život a zejména výpočty stavebních konstrukcí.
Ve stavební mechanice se tento komplexní soubor událostí nazývá podpůrná reakce. Má se za to, že když působíme silou (soustředěným zatížením) na podporu (viz obr. 4.1), dojde k reakci podpory, která je číselně rovna působícímu zatížení a směřuje v opačném směru - krása! Pokud jsme tedy na podpěru aplikovali zatížení 1 Newton, pak na podpěře dojde také k reakci 1 Newton, zatímco na druhé podpěře není žádné zatížení, proto je reakce podpěry 0. Tento předpoklad nám umožňuje nahradit podpory, přesněji spojení podpory, reaktivními silami - reakcemi podpory. Pro usnadnění vnímání lze síly měřit v kilogramových silách, 1 kgf ≈ 10 N (přesněji 1 kgf = 9,81 N). A nyní, pokud vezmeme v úvahu paprsek visící ve vzduchu, pak aby paprsek nespadl, jinými slovy, aby byl ve stavu statické rovnováhy, stačí na paprsek vyvinout dvě stejné, ale opačně zaměřené síly. v jednu chvíli.
Obrázek 4.1. Nahrazení podporových článků reaktivními silami - podporové reakce.
Rovnice statické rovnováhy (projekce sil).
Všechno se zdá jednoduché, ale ve skutečnosti jsme použili všechny základní axiomy statiky:
1. S každým působením jednoho tělesa na jiné těleso vzniká v jiném tělese protipůsobení, které má stejnou hodnotu jako působení, ale směřuje opačně. V tomto případě je reakce reakcí nosiče.
2. Mechanický stav tělesa se nezmění, pokud se těleso uvolní z vazeb a na stejné body tělesa působí síly rovné reakčním silám vazeb, které na ně působily. V tomto případě jsme podpěry nahradili podpěrnými reakcemi.
3. Pokud je těleso pod vlivem soustavy sil v rovnovážném stavu (v klidu) nebo pokračuje v pohybu konstantní rychlostí, pak je taková soustava sil vyvážená.
Můžeme tedy sestavit první dvě rovnice, které splňují podmínky statické rovnováhy systému:
∑ y \u003d Q - R lev - R pr \u003d 0(5.1) - pro síly působící podél osy v.
∑ x = 0(5.2) - pro síly (které v tomto případě chybí) působící podél osy X.
Poznámka: protože v tomto případě neexistují žádné horizontální síly, reakce horizontální podpory RH lev = 0, při nahrazení podpěrných článků reaktivními silami, není znázorněno pro zjednodušení vnímání.
Všechny nás ve škole učili, že os X probíhá vodorovně a os v- vertikálně tuto tradici neporušíme (i když to nemá zásadní význam). Vzhledem k tomu, že reakce na pravé podpěře je nulová, ukazuje se, že reakce na levé podpěře je rovna působící síle - to je také jeden z axiomů statiky:
4. Dvě síly působící na určité těleso jsou považovány za vyvážené právě tehdy, pokud jsou stejné velikosti a působí v jedné přímce v opačných směrech.
5. Aniž by došlo k porušení rovnovážného stavu tělesa, lze na něj působit nebo mu odebírat jakýkoli vyvážený systém sil.
4.1. Definice podpůrných reakcí.
Nyní si úkol trochu zkomplikujeme. Naše pravítko (tedy nosník) leží na dvou podpěrách a když prstem zatlačíme mezi podpěry na pravítku, a vědecky řečeno, působíme soustředěně, pak dojde k reakci na obou podpěrách. Protože statickou rovnováhu soustavy můžeme pozorovat i pouhým okem, je logické předpokládat, že celková reakce podpor je číselně rovna působícímu zatížení. Hodnotu reakcí podpor můžete určit jednoduchou grafickou metodou (podle vlivu):
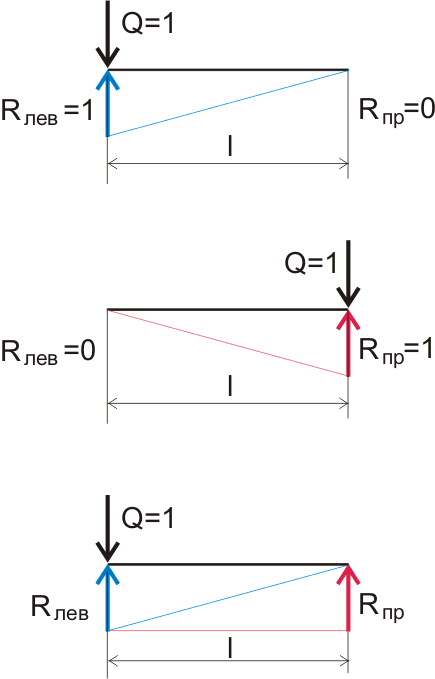
Obrázek 5.2. Grafické zobrazení změny reakcí podpor v závislosti na vzdálenosti působení zatížení.
Pokud na levou podpěru působíme zatížením Q = 1 kgf, pak reakce na levé podpěře (v grafu vyznačeno modře) bude Rlev = 1 kgf a na pravé podpěře R pr = 0 kgf. Pokud tyto hodnoty zkombinujeme, dostaneme pravoúhlý trojúhelník, ve kterém spodní rameno je délka nosníku, druhé rameno je reakce na podpěře, na kterou působí zatížení, přepona v tomto případě ukazuje změnu v reakci podpory po délce nosníku se tato čára nazývá vliv čáry. Pokud znázorníme totéž pro reakci na pravé podpoře, dostaneme přesně stejný trojúhelník, ale pro názornost jej znázorníme obráceně. V důsledku toho jsme dostali pravidelný obdélník o dvou pravoúhlé trojúhelníky, ale ve skutečnosti se jedná o magický obdélník (nomogram), který vám bez zvláštních výpočtů umožňuje určit reakci na jakoukoli podporu v závislosti na místě působení zatížení:
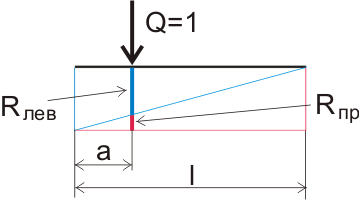
Obrázek 5.3. Grafické vymezení podpůrné reakce.
Například vzdálenost mezi knihami je 20 cm. To znamená, že vzdálenost mezi podpěrami (rozpětí našeho nosníku) je 20 cm a v obecném případě l . Délka paprsku se měří podél osy X. Pokud aplikujeme soustředěné zatížení v určité vzdálenosti od levé podpory, označíme ji písmenem A, pak se reakční hodnota levé podpěry bude rovnat délce segmentu nakresleného kolmo k dlouhému ramenu modrého trojúhelníku a reakční hodnota pravé podpěry je délka segmentu nakresleného kolmo k dlouhému ramenu modrého trojúhelníku. červený trojúhelník. V součtu jsou to jedna, protože jsme vzali hodnotu zatížení rovnou 1.
Můžete také určit reakci podpor pomocí matematických vzorců popisujících úměrnost pravoúhlých trojúhelníků: Pokud je zatížení aplikováno na vzdálenost A z podpory na Celková délka trámy l , pak reakce na správnou podporu bude:
R pr \u003d B \u003d Qa / l (4.1)
a reakce na levé podpoře bude:
R lev \u003d A \u003d Q (l - a) / l (4.2)
Při počítání samozřejmě každý používá vzorce, ale i tak nám přijde vhod přehlednost trojúhelníků.
Při určování reakce podpor z působení rozložené zatížení, nejprve se určí výsledná síla, tzn. rozložené zatížení se redukuje na soustředěné a poté se určí reakce podpor v závislosti na místě působení soustředěného zatížení. Pokud je rozložené zatížení rovnoměrně rozloženo a působí po celé délce nosníku, pak budou reakce podpor A = B = ql / 2. Jak určit reakce podpory v jiných případech, doufám, bude zřejmé z dalšího popisu.
Rovnice ohybového momentu, třetí rovnice statické rovnováhy soustavy
Pokud na knihy položíme pravítko 20 cm a zatlačíme prstem doprostřed, pravítko se ohne o určitou vzdálenost, pokud vezmeme pravítko 40 cm ze stejné části a ze stejného materiálu, opřeme ho o knihy naskládat ve vzdálenosti 40 cm a aplikovat na pravítko přesně stejnou zátěž, vzdálenost o kterou se pravítko ohne bude větší, o co jde? vždyť se nezměnilo ani zatížení, ani materiál nosníku, ani průřez nosníku, změnila se pouze délka nosníku.
Stavební mechanika vysvětluje tento zázrak následovně: síly působící na nosník jsou jedna věc, ale ohybový moment, který vzniká v uvažovaném průřezu působením síly, je věc úplně jiná.
Všichni si pamatujeme Archiméda a jeho radost z objevu principu páky, a tak tento princip funguje všude, jeho podstata se scvrkává na následující: čím větší je páka, tím menší sílu lze použít k provedení stejné práce.
V teoretické a strukturální mechanice se jako správnější používá pojem ramene síly, takže se má za to, že vnitřní napětí vznikající v průřezu nosníku při působení zatížení jsou přímo úměrné rameni. působící síly. A to znamená, že podpěrné reakce jsou síly, které se snaží ohnout paprsek, zatímco osou páky je naše soustředěné zatížení. Taková změna hodnoty momentu v závislosti na rameni síly se v matematice nazývá změna hodnoty funkce v závislosti na proměnné X, tak se ukazuje, že hodnotu momentu v libovolném bodě našeho paprsku lze popsat rovnicí M = Px. Zdá se, že vzorec není složitý, ale velmi důležitý.
Ukazuje se, že v řezu nosníku od počátku do místa působení síly Q působí na nosník pouze jedna síla - reakce podpěry R lev (pro zjednodušení jsou často naznačeny reakce na podpěrách velkými písmeny, protože existuje mnoho podpěr, je obvyklé označit podpěru zcela vlevo - " ALE") a momentová rovnice v této části bude vypadat takto:
M = Ah(0≤ x< a) (6.1)
a v řezu za bodem působení síly Q na konec nosníku působí na nosník dvě síly - reakce podpěry A a samotná síla Q a potom bude momentová rovnice vypadat takto:
M \u003d Ah – Q (x – a)(a ≤ x< l) (6.2)
V bodě B na pravé podpěře nosníku bude momentová rovnice vypadat takto:
M B \u003d Al - Q (l - a) + B (l - l)(x = l) (6,3)
Tyto rovnice popisují statickou rovnováhu systému. Například na kloubové podpěry neexistuje žádný ohybový moment a skutečně, řešení rovnice (6.1) v x = 0 nám dává 0 a řešení rovnice (6.3) v x = l nám dává stejnou 0. Rovnice (6.3) je tedy třetí rovnicí statické rovnováhy a lze jej zapsat v následujícím tvaru:
ΣM B \u003d Al - Q (l - a) \u003d 0 (6.4)
A také rovnice (6.1) a (6.2) umožňují určit hodnotu momentu v libovolném bodě nosníku, a přesněji pak v jakémkoli uvažovaném průřezu nosníku. Navíc při řešení těchto rovnic používáme metodu řezů, která je diskutována níže, ale nyní uvažujme následující názorný příklad:
Nosník na dvou sklopných podpěrách.
7.1. U nosníku, na který působí soustředěné zatížení uprostřed nosníku, je snadné určit ohybový moment v libovolném bodě průřezu na levé části nosníku: musíte vynásobit reakci jedné z podpor vzdáleností od této podpory k místu působení zatížení (na řezu nosníku od x \u003d 0 do x=l/2). Z matematického hlediska to bude vypadat takto:
M = (Q/2)x (7.1)
Protože v tomto případě je reakce každé z podpor rovna polovině aktuálního zatížení. Maximální hodnota ohybového momentu bude také uprostřed, tzn. ve vzdálenosti l/2 od začátku paprsku a bude:
M = (Q/2) (1/2) = Ql/4 (7.2)
Kompletní momentová rovnice v oblasti kde l/2< x < l , выглядит так:
∑M x \u003d (Q / 2) x - Q (x - l / 2)(7.3)
Působením zatížení a reakcí podpor působí na nosník ohybový moment a hodnota tohoto ohybového momentu pro každý bod, respektive průřez nosníku, je různá. V podpěrných bodech je ohybový moment 0, bez ohledu na to, kde působí zatížení, protože naše podpěry jsou kloubové. Maximální ohybový moment působí v jednom z průřezů nosníku, když uprostřed působí soustředěné zatížení.
Pro názornost je při řešení statických problémů zvykem stavět "epury" ohybového momentu a působících sil, takže později by bylo snazší určit polohu průřezu, ve kterém je maximální příčná nebo podélná síla nebo ohyb moment působí. Ve svém jádru jsou diagramy grafy funkcí popsaných odpovídajícími rovnicemi. Pokud je například zatížení aplikováno uprostřed nosníku, budou diagramy vypadat takto:
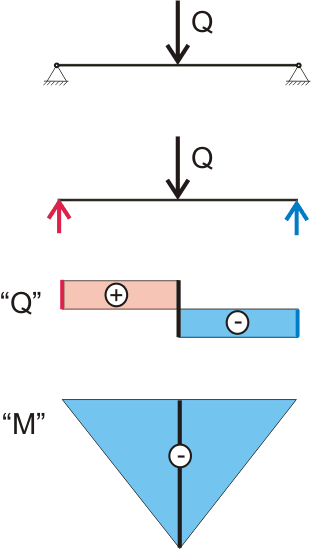
Obrázek 7.1. Grafy příčných sil a momentů působících v průřezech nosníku.
Graf "Q" zobrazuje změnu sil působících na nosník, respektive změnu smykových napětí v průřezech nosníku. Takže podle našeho diagramu je vidět, že na začátku paprsku se hodnota diagramu prudce změní z 0 na Q/2 Toto je podpůrná reakce. Uprostřed nosníku, kde působí síla Q, hodnota diagramu se prudce změní o hodnotu " Q"a teď je - Q/2, na konci nosníku, druhá reakce podpory rovna Q/2, tím se hodnota grafu změní z - Q/2 na 0 . Značky "+" a "-" znamenají směr působení sil. Pokud síla směřuje nahoru (rovnoběžně s osou v), pak se taková síla považuje za kladnou, pokud síla směřuje dolů, pak se taková síla považuje za zápornou.
Diagram "M" zobrazuje změnu ohybového momentu působícího na nosník, respektive změnu normálových napětí v průřezech nosníku (o vnitřních napětích, normálových a tečných, budeme hovořit dále). Takže podle našeho diagramu je vidět, že na začátku nosníku je ohybový moment 0 a to je logické, protože rameno síly, v tomto případě podpěrná reakce, je rovna nule, pak hodnota ohybu moment roste úměrně se změnou délky ramene síly. Uprostřed nosníku, kde působí síla Q, na diagramu "M" je pozorován zlom, protože do hry vstupuje další síla - aplikované koncentrované zatížení, které je 2krát větší, pokud jde o hodnotu reakce podpory.
Dále působením dvou opačně nasměrovaných, působících v různých bodech a nestejnoměrných sil, se hodnota ohybového momentu snižuje a na konci nosníku na pravé podpoře je hodnota ohybového momentu opět 0. Z diagramu Obr. ohybových momentů můžete vizuálně určit hodnotu maximálního ohybového momentu v průřezu nosníku.
V tomto případě je vše jednoduché a bylo by docela možné obejít se bez diagramů, ale v budoucnu, pokud musíte vzít v úvahu vliv různých zatížení, včetně rozložených, pro nosník na několika podpěrách nebo s skřípnuté konce, přítomnost správně konstruovaného diagramu ohybového momentu pomůže přesně určit polohu průřezu nosníku (a nejen nosníku), ve kterém je ohybový moment maximální.
I bez dlouhých matematických výpočtů je vidět, že čím blíže je místo působení zatížení ke středu nosníku, tím větší je hodnota momentu a tím blíže je místo působení síly k jedné z podpor, čím blíže je hodnota momentu nule, a to je logické, maximální moment nastává při maximálním rameni síly, proto při výpočtu nosníku pro dynamicky se pohybující soustředěná zatížení (například lidé budou chodit po nosníku nebo kolo automobilu bude spočívat na nosníku), není třeba počítat průřez nosníku pro všechny polohy zatížení, stačí vypočítat nosník pro zatížení působící v nejslabším místě - uprostřed.
V tomto případě není znak "-" na diagramu momentů nic jiného než konvence. Ať je směr působení momentu jakýkoli, v uvažovaném průřezu bude vždy jak natažená, tak stlačená zóna. V tomto případě schéma ukazuje, že spodní část úseku bude natažena. Obecně je moment považován za kladný, pokud se pokusí otočit paprsek ve směru hodinových ručiček vzhledem k uvažovanému bodu řezu. Někdy se to považuje za opak, ale nejde o nic jiného než o pohodlnost. V tomto případě již diagram momentů ukazuje, zda se paprsek bude ohýbat nahoru nebo dolů, bez vykreslení úhlů natočení a průhybů (o těchto diagramech budeme hovořit o něco později). Jinými slovy, mnohem důležitější je pochopit, kde v důsledku zatížení dojde ke stlačení a kde, tahové zóně průřezu nosníku, je znaménko momentu druhořadé.
Pokud vezmeme stejné pravítko, jeden konec pravítka zapíchneme mezi knihy a nejlépe mezi cihly a druhý konec necháme viset, získáme model konzolový nosník. Zvláštností konzolového nosníku je to, že má pouze jednu podpěru a tuhé sevření neumožňuje nosníku volně se otáčet kolem této podpory. Protože existuje pouze jedna podpora, bez ohledu na to, kde působíme zatížení na nosník, bude reakce podpory vždy rovna působícímu zatížení. Pokud se, jako v případě nosníku na kloubových podpěrách, pokusíme odstranit podpěru a nahradit ji reakcí, pak nebude splněna podmínka rovnováhy systému, dvě stejné hodnoty, opačně zaměřené síly, které neleží na jedné přímce otočí paprsek kolem určitého bodu "o":
Obrázek 8.1. Výskyt krouticího momentu při působení stejných sil v různých bodech.
Jak je patrné z obrázku 8.1 a z popisu povahy okamžiku je zřejmé, než větší vzdálenost mezi body působení sil, tím větší bude točivý moment. Abychom dodrželi rovnovážnou podmínku soustavy, potřebujeme na nosník vyvinout další krouticí moment, tzn. další dvojice sil, která se pokusí otočit paprsek v opačném směru.
Ohybový moment vznikající na tuhé podpoře konzolového nosníku při působení soustředěného zatížení:
M = -Qx (8.1)
Ohybový moment, který vzniká na tuhé podpěře konzolového nosníku působením rozloženého zatížení po celé délce nosníku:
M = -(ql)l/2 = -ql2/2 (8.2)
To lze znázornit na diagramu pomocí symbol ohybový moment (nám známý z prvního dílu), nás ale nyní zajímají specifika. Vzhledem k tomu, že náš paprsek má celkem hmatatelnou výšku a šířku, bylo by logické aplikovat tyto síly na paprsek, přesněji řečeno na průřez nosníku, a zde i pouhým okem je vidět, že čím větší výška nosníku, menší síly mohou být aplikovány úplně nahoře a úplně dole na nosníku, takže hodnota momentu je stejná:
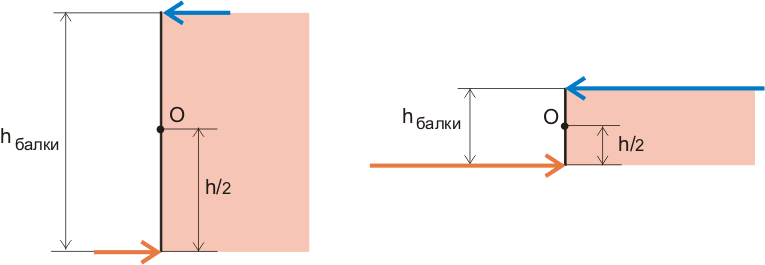
Obrázek 8.2. Nárůst hodnoty sil s poklesem výšky nosníku při stejném momentu.
V tomto případě se horní síla snaží paprsek natáhnout a spodní síla paprsek stlačit. Zdá se, že zde není nic složitého, vše je docela jednoduché a srozumitelné, ale ve skutečnosti jsme objevili nejdůležitější tajemství sopromatu:
Ohybový moment působící na libovolný stavební konstrukce v určitém bodě lze považovat za dvojici sil působících na průřez nosníku v tomto bodě.
Sekční metoda
Tento přístup nám umožňuje při řešení úloh uvažovat nikoli celý nosník, ale pouze jeho část, přičemž chybějící část nahradíme dvojicí sil působících na průřez nosníku. Takže jsme například nemohli uvažovat celý nosník (obrázek 7.2), ale pouze pravou polovinu, přičemž levou polovinu nahradil moment nebo pár sil.
A pokud jsou v uvažovaném průřezu tangenciální napětí určená diagramem příčných sil a (nebo) normálová napětí určená diagramem normálových sil, pak aby byla řezná část nosníku v rovnováze, všechna tato zatížení musíme aplikovat na uvažovaný příčný řez.
Toto je podstata metody sekcí:
- Při řešení úloh neuvažujeme celý nosník, ale pouze jeho část odříznutou průřezem.
- Aby tato část zůstala ve stavu statické rovnováhy, musíme v uvažovaném průřezu působit vnějšími silami.
- Vnitřní napětí, která v uvažovaném průřezu vznikají, jsou reakcí materiálu na působení vnějších sil.
Řešením výše uvedených rovnic tedy určíme hodnoty vnějšího ohybového momentu a nyní je čas zjistit, jaká na to bude reakce materiálu.
V tomto případě jsme aplikovali síly úplně nahoře a úplně dole na nosníku (obrázek 8.2), ale tyto síly můžeme aplikovat v libovolném bodě průřezu nosníku, hlavní je, že hodnota vnější moment se nemění. Soustředěné síly lze nahradit rozloženým zatížením, které vytvoří stejný ohybový moment, přičemž hodnota rozloženého zatížení se může lišit v závislosti na výšce nosníku a lze ji graficky znázornit následovně:
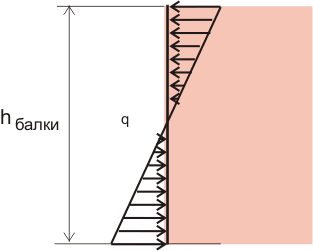
Obrázek 8.3. Změna rozloženého zatížení podél výšky nosníku.
Proč má rozložení normálových napětí po výšce průřezu nosníku tak zvláštní podobu, nyní zjistíme.
Platnost reakce podporuje odkazuje na elastické síly a je vždy směrován kolmo k povrchu. Působí proti jakékoli síle, která způsobuje pohyb těla kolmo k podpěře. Abyste ji mohli vypočítat, musíte identifikovat a zjistit číselnou hodnotu všech sil, které působí na těleso stojící na podpěře.
Budete potřebovat
- - váhy;
- - rychloměr nebo radar;
- - goniometr.
Návod
- Určete tělesnou hmotnost pomocí vah nebo jakýmkoli jiným způsobem. Pokud je těleso na vodorovné ploše (a je jedno, zda se pohybuje nebo je v klidu), pak se reakční síla podpěry rovná gravitační síle působící na těleso. Chcete-li to vypočítat, vynásobte hmotnost těla gravitačním zrychlením, které se rovná 9,81 m / s² N \u003d m g.
- Když se těleso pohybuje po nakloněné rovině nasměrované pod úhlem k horizontu, reakční síla podpory je pod úhlem gravitace. Přitom kompenzuje pouze tu složku gravitace, která působí kolmo na nakloněnou rovinu. Pro výpočet reakční síly podpěry použijte goniometr k měření úhlu, pod kterým je rovina umístěna k horizontu. Vypočítat síla podporují reakce vynásobením hmotnosti těla zrychlením volného pádu a kosinusem úhlu, pod kterým rovina svírá horizont N=m g Cos(α).
- V případě, že se těleso pohybuje po povrchu, který je součástí kružnice o poloměru R, např. most, návrší, pak reakční síla podpěry zohledňuje sílu působící ve směru od střed kruhu, se zrychlením rovným dostředivému, působícímu na těleso. Chcete-li vypočítat reakční sílu podpory v nejvyšším bodě, odečtěte poměr druhé mocniny rychlosti k poloměru zakřivení trajektorie od gravitačního zrychlení.
- Výsledné číslo vynásobte hmotností pohybujícího se tělesa N=m (g-v²/R). Rychlost by se měla měřit v metrech za sekundu a poloměr v metrech. Při určité rychlosti se hodnota zrychlení směrovaného ze středu kruhu může rovnat a dokonce převyšovat zrychlení volného pádu, v tomto okamžiku adheze těla k povrchu zmizí, proto například motoristé potřebují jasně řídit rychlost na takových úsecích silnice.
- Pokud zakřivení směřuje dolů a trajektorie těla je konkávní, pak vypočítejte reakční sílu podpěry sečtením poměru druhé mocniny rychlosti a poloměru zakřivení trajektorie ke zrychlení volného pádu a výsledný výsledek vynásobte tělesnou hmotností N=m (g+v2/R).
- Pokud jsou známy třecí síla a koeficient tření, vypočítejte reakční sílu podpěry vydělením třecí síly tímto koeficientem N=Ftr/μ.