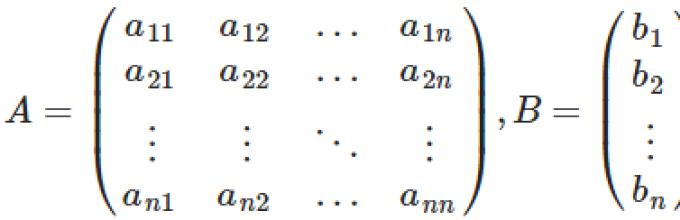نظم المعادلات الخطية من الرتبة الثانية والثالثة. كيفية إيجاد حل عام وخاصة لنظام المعادلات الخطية

طريقة المصفوفة حلول SLAUتستخدم لحل أنظمة المعادلات التي يتوافق فيها عدد المعادلات مع عدد المجهول. أفضل طريقة لاستخدامها في حل الأنظمة ذات الترتيب المنخفض. تعتمد طريقة المصفوفة لحل أنظمة المعادلات الخطية على تطبيق خصائص ضرب المصفوفة.

بهذه الطريقة ، بعبارة أخرى طريقة المصفوفة العكسيةيسمى كذلك ، نظرًا لأن الحل يتم اختزاله إلى معادلة المصفوفة المعتادة ، والتي تحتاج إلى إيجاد حلها المعكوس المصفوفة.

طريقة حل المصفوفة SLAE مع محدد أكبر من أو أقل من الصفر كما يلي:

افترض أن هناك SLE (نظام المعادلات الخطية) مع نغير معروف (فوق حقل تعسفي):

لذلك ، من السهل ترجمتها إلى شكل مصفوفة:

AX = ب، أين أهي المصفوفة الرئيسية للنظام ، بو X- أعمدة الأعضاء الأحرار وحلول النظام على التوالي:

اضرب معادلة المصفوفة الموجودة على اليسار في أ -1- معكوس المصفوفة إلى المصفوفة أ: أ -1 (أ) = أ -1 ب.

لان أ −1 أ = هـ، يعني، س = أ -1 ب. يعطي الجانب الأيمن من المعادلة عمودًا من الحلول للنظام الأولي. شرط قابلية تطبيق طريقة المصفوفة هو عدم تجدد المصفوفة أ. الشرط الضروري والكافي لذلك هو محدد المصفوفة أ:

تفصيل أ ≠ 0.

ل نظام متجانس من المعادلات الخطية، بمعنى آخر. إذا كان ناقل ب = 0، إجراء حكم عكسي: في النظام AX = 0هو حل غير تافه (أي لا يساوي الصفر) فقط عندما ديتا = 0. يسمى هذا الارتباط بين حلول الأنظمة المتجانسة وغير المتجانسة للمعادلات الخطية بديل لفريدهولم.

وبالتالي ، يتم إجراء حل SLAE بطريقة المصفوفة وفقًا للصيغة . أو ، تم العثور على حل SLAE باستخدام مصفوفة معكوسة أ -1.

من المعروف أن مصفوفة مربعة لكنطلب نعلى ال نهناك معكوس المصفوفة أ -1فقط إذا كان محدده غير صفري. هكذا النظام نالمعادلات الجبرية الخطية مع نيتم حل المجهول بطريقة المصفوفة فقط إذا كان محدد المصفوفة الرئيسية للنظام لا يساوي الصفر.

على الرغم من وجود قيود على إمكانية استخدام هذه الطريقة وهناك صعوبات حسابية للقيم الكبيرة للمعاملات والأنظمة عالية الترتيب ، يمكن تنفيذ هذه الطريقة بسهولة على الكمبيوتر.

مثال على حل غير متجانسة SLAE.

أولاً ، دعنا نتحقق مما إذا كانت محددات مصفوفة المعاملات لـ SLAEs غير معروفة لا تساوي الصفر.

الآن نجد مصفوفة التحالف، اقلبها واستبدلها بالصيغة لتحديد معكوس المصفوفة.

نستبدل المتغيرات في الصيغة:

نوجد الآن المجهول بضرب معكوس المصفوفة وعمود الحدود الحرة.

لذا، س = 2 ؛ ص = 1 ؛ ض = 4.

عند الانتقال من الشكل المعتاد لـ SLAE إلى نموذج المصفوفة ، كن حذرًا مع ترتيب المتغيرات غير المعروفة في معادلات النظام. علي سبيل المثال:

لا تكتب كـ:

من الضروري ، أولاً ، ترتيب المتغيرات غير المعروفة في كل معادلة للنظام وفقط بعد ذلك انتقل إلى تدوين المصفوفة:

بالإضافة إلى ذلك ، يجب أن تكون حريصًا عند تعيين المتغيرات غير المعروفة ، بدلاً من × 1 ، × 2 ، ... ، × نقد تكون هناك رسائل أخرى. علي سبيل المثال:

في شكل مصفوفة نكتب:

من الأفضل حل الأنظمة باستخدام طريقة المصفوفة المعادلات الخطية، حيث يتطابق عدد المعادلات مع عدد المتغيرات غير المعروفة ويكون محدد المصفوفة الرئيسية للنظام لا يساوي الصفر. عندما يكون هناك أكثر من 3 معادلات في النظام ، سوف يتطلب الأمر مزيدًا من الجهد الحسابي للعثور على معكوس المصفوفة ، لذلك ، في هذه الحالة ، يُنصح باستخدام طريقة Gauss لحلها.

تستخدم أنظمة المعادلات على نطاق واسع في الصناعة الاقتصادية في النمذجة الرياضية للعمليات المختلفة. على سبيل المثال ، عند حل مشاكل الإدارة وتخطيط الإنتاج ، فإن الطرق اللوجستية ( مهمة النقل) أو وضع المعدات.

تستخدم أنظمة المعادلات ليس فقط في مجال الرياضيات ، ولكن أيضًا في الفيزياء والكيمياء وعلم الأحياء ، عند حل مشاكل تحديد حجم السكان.

نظام المعادلات الخطية هو مصطلح لمعادلتين أو أكثر مع العديد من المتغيرات التي من الضروري إيجاد حل مشترك لها. مثل هذا التسلسل من الأرقام حيث تصبح جميع المعادلات مساواة حقيقية أو تثبت أن التسلسل غير موجود.

معادلة خط مستقيم

المعادلات من الشكل ax + by = c تسمى الخطية. التعيينات س ، ص هي المجهول ، التي يجب إيجاد قيمتها ، ب ، أ هي معاملات المتغيرات ، ج هو المصطلح المجاني للمعادلة.
سيبدو حل المعادلة برسم التمثيل البياني الخاص بها كخط مستقيم ، وجميع نقاطه تمثل حل كثير الحدود.

أنواع أنظمة المعادلات الخطية

أبسط أمثلة لأنظمة المعادلات الخطية بمتغيرين X و Y.

F1 (x، y) = 0 و F2 (x، y) = 0 ، حيث F1،2 هي وظائف و (x، y) متغيرات دالة.

حل جملة معادلات - يعني العثور على هذه القيم (س ، ص) التي يصبح النظام مساواة حقيقية لها ، أو لإثبات عدم وجود قيم مناسبة لـ x و y.

زوج من القيم (س ، ص) ، مكتوب على هيئة إحداثيات نقطية ، يسمى حل لنظام المعادلات الخطية.

إذا كان للأنظمة حل واحد مشترك أو لا يوجد حل ، فيُطلق عليها مكافئ.

الأنظمة المتجانسة للمعادلات الخطية هي الأنظمة التي يكون جانبها الأيمن مساويًا للصفر. إذا كان الجزء الأيمن بعد علامة "يساوي" له قيمة أو يتم التعبير عنه بواسطة دالة ، فإن هذا النظام ليس متجانسًا.

يمكن أن يكون عدد المتغيرات أكثر من متغيرين ، ثم يجب أن نتحدث عن مثال لنظام المعادلات الخطية مع ثلاثة متغيرات أو أكثر.

في مواجهة الأنظمة ، يفترض تلاميذ المدارس أن عدد المعادلات يجب أن يتطابق بالضرورة مع عدد المجهول ، لكن هذا ليس كذلك. لا يعتمد عدد المعادلات في النظام على المتغيرات ، يمكن أن يكون هناك عدد كبير منهم بشكل تعسفي.

طرق بسيطة ومعقدة لحل أنظمة المعادلات

لا يوجد مشترك المنهج التحليليحلول الأنظمة المتشابهة ، جميع الطرق تعتمد على الحلول العددية. يصف مقرر الرياضيات المدرسية بالتفصيل طرق مثل التقليب ، الجمع الجبري ، الاستبدال ، وكذلك طريقة الرسوم البيانية والمصفوفة ، الحل بطريقة غاوس.

تتمثل المهمة الرئيسية في طرق التدريس في الحل في تعليم كيفية تحليل النظام بشكل صحيح وإيجاد خوارزمية الحل الأمثل لكل مثال. الشيء الرئيسي ليس حفظ نظام من القواعد والإجراءات لكل طريقة ، ولكن لفهم مبادئ تطبيق طريقة معينة.

حل أمثلة لأنظمة المعادلات الخطية للفئة السابعة من البرنامج .مدرسة ثانويةبسيطة للغاية وموضحة بتفصيل كبير. في أي كتاب مدرسي عن الرياضيات ، يحظى هذا القسم بالاهتمام الكافي. تمت دراسة حل أمثلة أنظمة المعادلات الخطية بطريقة Gauss و Cramer بمزيد من التفصيل في الدورات الأولى لمؤسسات التعليم العالي.

حل الأنظمة بطريقة الاستبدال

تهدف إجراءات طريقة الاستبدال إلى التعبير عن قيمة متغير واحد من خلال الثاني. يتم استبدال التعبير في المعادلة المتبقية ، ثم يتم تقليله إلى شكل متغير واحد. يتم تكرار الإجراء اعتمادًا على عدد المجهول في النظام

دعنا نعطي مثالاً لنظام المعادلات الخطية من الفئة السابعة بطريقة الاستبدال:

كما يتضح من المثال ، تم التعبير عن المتغير x من خلال F (X) = 7 + Y. ساعد التعبير الناتج ، الذي تم استبداله في المعادلة الثانية للنظام بدلاً من X ، في الحصول على متغير واحد Y في المعادلة الثانية . قرار هذا المثاللا يسبب صعوبات ويسمح لك بالحصول على قيمة Y. الخطوة الأخيرة هي التحقق من القيم المستلمة.

ليس من الممكن دائمًا حل مثال لنظام المعادلات الخطية بالتعويض. يمكن أن تكون المعادلات معقدة والتعبير عن المتغير من حيث المجهول الثاني سيكون مرهقًا جدًا لإجراء المزيد من العمليات الحسابية. عندما يكون هناك أكثر من 3 مجاهيل في النظام ، يكون حل الاستبدال غير عملي أيضًا.

حل مثال لنظام المعادلات الخطية غير المتجانسة:

الحل باستخدام الجمع الجبري

عند البحث عن حل للأنظمة بطريقة الإضافة ، يتم إجراء عملية الجمع مصطلحًا بمصطلح وضرب المعادلات بأرقام مختلفة. الهدف النهائي للعمليات الحسابية هو معادلة ذات متغير واحد.

تتطلب تطبيقات هذه الطريقة الممارسة والمراقبة. ليس من السهل حل نظام المعادلات الخطية باستخدام طريقة الجمع مع عدد المتغيرات 3 أو أكثر. تكون الجمع الجبري مفيدة عندما تحتوي المعادلات على كسور وأرقام عشرية.

خوارزمية عمل الحل:

1. اضرب طرفي المعادلة بعدد ما. نتيجة للعملية الحسابية ، يجب أن يصبح أحد معاملات المتغير مساويًا لـ 1.
2. أضف المصطلح الناتج عن طريق المصطلح وابحث عن أحد المجهولين.
3. عوّض بالقيمة الناتجة في المعادلة الثانية للنظام لإيجاد المتغير المتبقي.

طريقة الحل بإدخال متغير جديد

يمكن إدخال متغير جديد إذا احتاج النظام إلى إيجاد حل لما لا يزيد عن معادلتين ، كما يجب ألا يزيد عدد المجاهيل عن اثنين.

تستخدم الطريقة لتبسيط إحدى المعادلات بإدخال متغير جديد. يتم حل المعادلة الجديدة فيما يتعلق بالمجهول الذي تم إدخاله ، ويتم استخدام القيمة الناتجة لتحديد المتغير الأصلي.

يمكن أن نرى من المثال أنه من خلال إدخال متغير جديد t ، كان من الممكن تقليل المعادلة الأولى للنظام إلى مربع قياسي ثلاثي الحدود. يمكنك حل كثير الحدود بإيجاد المميز.

من الضروري إيجاد قيمة المميز باستخدام الصيغة المعروفة: D = b2 - 4 * a * c ، حيث D هو المميز المطلوب ، b ، a ، c هي مضاعفات كثير الحدود. في المثال المعطى ، أ = 1 ، ب = 16 ، ج = 39 ، ومن ثم د = 100. إذا كان المميز أكبر من الصفر ، فهناك حلان: t = -b ± √D / 2 * a ، إذا كان المميز أقل من الصفر ، فهناك حل واحد فقط: x = -b / 2 * a.

تم العثور على حل الأنظمة الناتجة عن طريق طريقة الجمع.

طريقة بصرية لحل النظم

مناسب للأنظمة ذات 3 معادلات. تتكون الطريقة من رسم الرسوم البيانية لكل معادلة مدرجة في النظام على محور الإحداثيات. ستكون إحداثيات نقاط تقاطع المنحنيات هي الحل العام للنظام.

طريقة الرسم لديها عدد من الفروق الدقيقة. ضع في اعتبارك عدة أمثلة لحل أنظمة المعادلات الخطية بطريقة مرئية.

كما يتضح من المثال ، تم إنشاء نقطتين لكل سطر ، تم اختيار قيم المتغير x بشكل عشوائي: 0 و 3. بناءً على قيم x ، تم العثور على قيم y: 3 و 0. تم تمييز النقاط ذات الإحداثيات (0 ، 3) و (3 ، 0) على الرسم البياني وتم توصيلها بخط.

يجب تكرار الخطوات للمعادلة الثانية. نقطة تقاطع الخطوط هي حل النظام.

في المثال التالي ، مطلوب إيجاد حل رسومي لنظام المعادلات الخطية: 0.5x-y + 2 = 0 and 0.5x-y-1 = 0.

كما يتضح من المثال ، ليس للنظام أي حل ، لأن الرسوم البيانية متوازية ولا تتقاطع بطولها بالكامل.

الأنظمة من الأمثلة 2 و 3 متشابهة ، ولكن عند بنائها ، يصبح من الواضح أن حلولها مختلفة. يجب أن نتذكر أنه ليس من الممكن دائمًا تحديد ما إذا كان النظام لديه حل أم لا ، فمن الضروري دائمًا إنشاء رسم بياني.

ماتريكس وأصنافها

تستخدم المصفوفات لكتابة نظام المعادلات الخطية بإيجاز. الجدول يسمى مصفوفة. نوع خاصمليئة بالأرقام. يحتوي n * m على n - صفوف و m - أعمدة.

تكون المصفوفة مربعة عندما يتساوى عدد الأعمدة والصفوف. متجه المصفوفة هو مصفوفة ذات عمود واحد مع عدد لا نهائي من الصفوف. تسمى المصفوفة التي تحتوي على وحدات على طول أحد الأقطار وعناصر صفرية أخرى متطابقة.

المصفوفة العكسية هي مثل هذه المصفوفة ، عندما يتم ضربها بحيث تتحول المصفوفة الأصلية إلى وحدة واحدة ، فإن مثل هذه المصفوفة توجد فقط للمربع الأول.

قواعد تحويل نظام المعادلات إلى مصفوفة

فيما يتعلق بأنظمة المعادلات ، تتم كتابة المعاملات والأعضاء الأحرار في المعادلات كأرقام من المصفوفة ، والمعادلة الواحدة هي صف واحد من المصفوفة.

يسمى صف المصفوفة non-zero إذا كان عنصر واحد على الأقل من الصف لا يساوي الصفر. لذلك ، إذا اختلف عدد المتغيرات في أي من المعادلات ، فمن الضروري إدخال صفر بدلاً من المجهول المفقود.

يجب أن تتوافق أعمدة المصفوفة بدقة مع المتغيرات. هذا يعني أنه لا يمكن كتابة معاملات المتغير x إلا في عمود واحد ، على سبيل المثال الأول ، معامل المجهول y - فقط في العمود الثاني.

عند ضرب مصفوفة ، يتم ضرب جميع عناصر المصفوفة بالتسلسل في رقم.

خيارات لإيجاد معكوس المصفوفة

صيغة إيجاد معكوس المصفوفة بسيطة للغاية: K -1 = 1 / | K | ، حيث K -1 هي معكوس المصفوفة و | K | - محدد المصفوفة. | ك | يجب ألا يكون مساويًا للصفر ، فإن النظام لديه حل.

يتم حساب المحدد بسهولة لمصفوفة 2 × 2 ، من الضروري فقط ضرب العناصر قطريًا ببعضها البعض. لخيار "ثلاثة في ثلاثة" ، توجد صيغة | K | = أ 1 ب 2 ج 3 + أ 1 ب 3 ج 2 + أ 3 ب 1 ج 2 + أ 2 ب 3 ج 1 + أ 2 ب 1 ج 3 + أ 3 ب 2 ج 1. يمكنك استخدام الصيغة ، أو تذكر أنك بحاجة إلى أخذ عنصر واحد من كل صف وكل عمود حتى لا تتكرر أرقام الأعمدة والصفوف الخاصة بالعناصر في المنتج.

حل أمثلة نظم المعادلات الخطية بطريقة المصفوفة

تتيح طريقة المصفوفة لإيجاد حل تقليل الإدخالات المرهقة عند حل الأنظمة التي تحتوي على عدد كبير من المتغيرات والمعادلات.

في هذا المثال ، nm هي معاملات المعادلات ، والمصفوفة متجه x n هي المتغيرات ، و b n هي المصطلحات المجانية.

حل الأنظمة بطريقة غاوس

في الرياضيات العليا ، تتم دراسة طريقة Gauss مع طريقة Cramer ، وتسمى عملية إيجاد حل للأنظمة طريقة حل Gauss-Cramer. تستخدم هذه الأساليب في البحث متغيرات النظاممع الكثير من المعادلات الخطية.

طريقة جاوس تشبه إلى حد بعيد حلول الاستبدال والجمع الجبرية ، ولكنها أكثر منهجية. في الدورة المدرسية ، يتم استخدام الحل Gaussian لأنظمة المعادلات 3 و 4. الغرض من هذه الطريقة هو تحويل النظام إلى شكل شبه منحرف مقلوب. من خلال عمليات التحويل والبدائل الجبرية ، تم العثور على قيمة متغير واحد في إحدى معادلات النظام. المعادلة الثانية عبارة عن تعبير به مجهولين ، و 3 و 4 - بمتغيرين 3 و 4 ، على التوالي.

بعد إحضار النظام إلى النموذج الموصوف ، يتم تقليل الحل الإضافي إلى الاستبدال المتسلسل للمتغيرات المعروفة في معادلات النظام.

في الكتب المدرسية للصف السابع ، يتم وصف مثال لحل غاوسي على النحو التالي:

كما يتضح من المثال ، في الخطوة (3) تم الحصول على معادلتين 3x3-2x 4 = 11 و 3x 3 + 2x 4 = 7. سيسمح لك حل أي من المعادلات بإيجاد أحد المتغيرات x n.

تقول النظرية 5 ، المذكورة في النص ، أنه إذا تم استبدال إحدى معادلات النظام بمعادلة مكافئة ، فسيكون النظام الناتج أيضًا مكافئًا للنظام الأصلي.

يصعب على الطلاب فهم طريقة جاوس المدرسة الثانوية، ولكنها من أكثر الطرق إثارة للاهتمام لتطوير براعة الأطفال المسجلين في البرنامج دراسة متعمقةفي فصول الرياضيات والفيزياء.

لسهولة تسجيل الحسابات ، من المعتاد القيام بما يلي:

تتم كتابة معاملات المعادلات والمصطلحات المجانية في شكل مصفوفة ، حيث يتوافق كل صف من المصفوفة مع إحدى معادلات النظام. يفصل الجانب الأيسر من المعادلة عن الجانب الأيمن. تشير الأرقام الرومانية إلى عدد المعادلات في النظام.

أولاً ، يكتبون المصفوفة التي يعملون بها ، ثم يتم تنفيذ جميع الإجراءات بأحد الصفوف. تتم كتابة المصفوفة الناتجة بعد علامة "السهم" وتستمر في إجراء العمليات الجبرية اللازمة حتى يتم تحقيق النتيجة.

نتيجة لذلك ، يجب الحصول على مصفوفة يكون فيها أحد الأقطار 1 ، وجميع المعاملات الأخرى تساوي صفرًا ، أي يتم تقليل المصفوفة إلى شكل واحد. يجب ألا ننسى إجراء حسابات بأرقام طرفي المعادلة.

هذا الترميز أقل تعقيدًا ويسمح لك بعدم تشتيت انتباهك من خلال سرد العديد من الأشياء المجهولة.

سيتطلب التطبيق المجاني لأي طريقة حل عناية وقدرًا معينًا من الخبرة. لم يتم تطبيق جميع الطرق. بعض طرق إيجاد الحلول مفضلة أكثر في مجال معين من النشاط البشري ، بينما توجد طرق أخرى لغرض التعلم.

الموضوع 2 حل أنظمة المعادلات الجبرية الخطية بالطرق المباشرة.

أنظمة المعادلات الجبرية الخطية (المختصرة باسم SLAE) هي أنظمة معادلات من النموذج

أو في شكل مصفوفة ،

أ × x = ب , (2.2)

أ - مصفوفة معاملات نظام الأبعاد ن ´ ن

x - ناقلات مجهولة تتكون من ن عنصر

ب - متجه الأجزاء الصحيحة من النظام ، ويتألف من ن عنصر.

أ = x = ب = (2.3)

حل SLAE عبارة عن مجموعة من ن الأرقام التي يتم استبدالها بالقيم x 1 , x 2 , … , x ن في النظام (2.1) يضمن أن الأطراف اليسرى متساوية مع الجانب الأيمن في جميع المعادلات.

كل SLAE اعتمادًا على قيم المصفوفات أ و ب قد يملك

حل واحد

العديد من الحلول بلا حدود

ليس حلا واحدا.

في هذه الدورة ، سننظر فقط في SLAEs التي لديها حل فريد. الشرط الضروري والكافي لذلك هو محدد المصفوفة أ .

للبحث عن حلول لأنظمة المعادلات الجبرية الخطية ، يمكن إجراء بعض التحولات التي لا تغير حلولها. التحولات المتكافئةتسمى أنظمة المعادلات الخطية مثل هذه التحولات التي لا تغير حلها. وتشمل هذه:

تبديل أي معادلتين في النظام (تجدر الإشارة إلى أنه في بعض الحالات ، المذكورة أدناه ، لا يمكن استخدام هذا التحويل) ؛

ضرب (أو قسمة) أي معادلة في النظام برقم لا يساوي الصفر ؛

الإضافة إلى معادلة واحدة لنظام من معادلته الأخرى ، مضروبة (أو مقسمة) في عدد غير صفري.

تنقسم طرق حل SLAE إلى مجموعتين كبيرتين ، تسمى - الطرق المباشرةو الطرق التكرارية. هناك أيضًا طريقة لتقليل مشكلة حل SLAE لمشكلة إيجاد الحد الأقصى لوظيفة من عدة متغيرات ، متبوعًا بحلها من خلال طرق العثور على أقصى حد (المزيد حول هذا عند الانتقال إلى الموضوع المقابل). توفر الطرق المباشرة الحل الدقيق للنظام (إن وجد) في خطوة واحدة. تجعل الطرق التكرارية (إذا تم ضمان تقاربها في نفس الوقت) من الممكن تحسين بعض التقريب الأولي بشكل متكرر للحل المطلوب لـ SLAE ، وبشكل عام ، لن تقدم حلًا دقيقًا أبدًا. ومع ذلك ، مع الأخذ في الاعتبار أن طرق الحل المباشر لا تقدم أيضًا حلولًا دقيقة بشكل مثالي بسبب أخطاء التقريب الحتمية في المراحل الوسيطة من الحسابات ، يمكن أيضًا أن توفر الطرق التكرارية نفس النتيجة تقريبًا.

الطرق المباشرة لحل SLAE. الطرق المباشرة الأكثر استخدامًا لحل SLAEs هي:

طريقة كرامر

طريقة جاوس (وتعديلها - طريقة جاوس-جوردان)

طريقة المصفوفة (باستخدام انعكاس المصفوفة أ ).

طريقة كرامر بناءً على حساب محدد المصفوفة الرئيسية أ ومحددات المصفوفة أ 1 , أ 2 , …, ا ن , التي تم الحصول عليها من المصفوفة أ استبدال واحد فيه ( أناث) العمود ( أنا= 1, 2,…, ن) إلى عمود يحتوي على عناصر متجه ب . بعد ذلك ، يتم تحديد حلول SLAE على أنها حاصل قسمة قيم هذه المحددات. أكثر دقة، الصيغ الحسابيةلديك هذا النوع

(2.4)

مثال 1. دعونا نجد من خلال طريقة كرامر حل SLAE من أجله

أ = , ب = .

نملك

أ 1 = , أ 2 = , أ 3 = , A4 = .

دعونا نحسب قيم محددات جميع المصفوفات الخمس (باستخدام وظيفة MOPRED للبيئة تتفوق). يحصل

منذ محدد المصفوفة أ لا يساوي الصفر - النظام لديه حل فريد. ثم نحدده بالصيغة (2.4). يحصل

طريقة جاوس. يتضمن حل SLAE بهذه الطريقة تجميع مصفوفة ممتدة للنظام أ * . المصفوفة المعززة للنظام هي مصفوفة الحجم نخطوط و ن+1 بما في ذلك المصفوفة الأصلية أ مع عمود مرفق به على اليمين يحتوي على المتجه ب .

أ* = (2.4)

هنا أ في + 1 = ب أنا (أنا = 1, 2, …, ن ).

جوهر طريقة جاوس هو التقليل (عن طريق التحولات المكافئة) من المصفوفة الممتدة للنظام إلى شكل مثلث (بحيث تكون العناصر الصفرية فقط أقل من قطرها الرئيسي).

أ * =

بعد ذلك ، بدءًا من السطر الأخير والتحرك لأعلى ، يمكننا تحديد قيم جميع مكونات الحل بالتسلسل.

بداية تحويلات المصفوفة الموسعة للنظام إلى النموذج المطلوب هي عرض قيم المعاملات في x 1 واختيار الصف الذي يحتوي فيه على أقصى قيمة مطلقة (هذا ضروري لتقليل حجم الخطأ الحسابي في الحسابات اللاحقة). يجب تبديل هذا الصف من المصفوفة المعززة بالصف الأول (أو الأفضل ، إضافة (أو طرح) إلى الصف الأول ووضع النتيجة في مكان الصف الأول). بعد ذلك ، يجب قسمة جميع عناصر هذا الصف الأول الجديد (بما في ذلك العناصر الموجودة في العمود الأخير) على هذا المعامل. بعد ذلك ، المعامل الذي تم الحصول عليه حديثًا أ 11 يصبح مساويا لواحد. بعيدًا عن كل من الصفوف المتبقية من المصفوفة ، من الضروري طرح صفها الأول مضروبًا في قيمة المعامل عند x 1 في هذا الخط (أي بالمبلغ أنا 1 ، أين أنا =2, 3, … ن ). بعد ذلك ، في جميع الصفوف ، بدءًا من الصفوف الثانية ، المعاملات عند x 1 (أي جميع المعاملات أنا 1 (أنا =2, …, ن ) ستكون صفرًا. نظرًا لأننا أجرينا تحويلات مكافئة فقط ، فلن يختلف حل SLAE الذي تم الحصول عليه حديثًا عن النظام الأصلي.

علاوة على ذلك ، مع ترك الصف الأول من المصفوفة دون تغيير ، سنقوم بتنفيذ جميع الإجراءات المذكورة أعلاه مع الصفوف المتبقية من المصفوفة ، ونتيجة لذلك ، المعامل الذي تم الحصول عليه حديثًا أ 22 يصبح مساويا للواحد وجميع المعاملات أنا 2 (أنا =3, 4, …, ن ) سيصبح صفرًا. استمرارًا لإجراءات مماثلة ، سنقوم في النهاية بإحضار المصفوفة الخاصة بنا إلى الشكل الذي تكون فيه جميع المعاملات أ الثاني = 1 (أنا =1, 2, …, ن) وجميع المعاملات aij = 0 (أنا =2, 3, …, ن, ي< أنا). إذا ، في خطوة ما ، عند البحث عن أكبر قيمة مطلقة للمعامل عند xj لن نتمكن من إيجاد معامل لا يساوي الصفر - وهذا يعني أن النظام الأصلي ليس لديه حل فريد. في هذه الحالة ، يجب إنهاء عملية اتخاذ القرار.

إذا انتهت عملية التحويلات المكافئة بنجاح ، فإن المصفوفة الممتدة "المثلثية" الناتجة سوف تتوافق مع النظام التالي من المعادلات الخطية:

من المعادلة الأخيرة لهذا النظام نجد القيمة x ن . علاوة على ذلك ، باستبدال هذه القيمة في المعادلة قبل الأخيرة ، نجد القيمة x ن -1 . بعد ذلك ، بالتعويض بكل من هاتين القيمتين الموجودتين في المعادلة الثالثة من أسفل النظام ، نجد القيمة x ن -2 . بالاستمرار في ذلك والتحرك على طول معادلة هذا النظام من الأسفل إلى الأعلى ، سنجد قيم الجذور الأخرى على التوالي. وأخيرًا ، استبدال القيم الموجودة x ن , x ن -1 , x ن -2 , x 3 و x 2 في المعادلة الأولى للنظام نجد القيمة × 1. يسمى هذا الإجراء للبحث عن قيم الجذور بواسطة المصفوفة المثلثية الموجودة إلى الوراء.تسمى عملية إحضار المصفوفة المعززة الأصلية بتحويلات مكافئة إلى شكل مثلث في خط مستقيمطريقة جاوس ..

يتم عرض خوارزمية مفصلة بشكل كافٍ لحل SLAE بطريقة Gauss في الشكل. .2.1 والشكل. 2.1 أ.

مثال 2. ابحث عن حل SLAE نفسه بطريقة Gauss ، والتي تم حلها بالفعل بواسطة طريقة Cramer. دعونا أولا نؤلف مصفوفته المعززة. يحصل

أ * = .

أولاً ، نتبادل الصفين الأول والثالث من هذه المصفوفة (حيث أن العمود الأول يحتوي على أكبر عنصر في القيمة المطلقة) ، ثم نقسم جميع عناصر هذا الصف الأول الجديد على القيمة 3. نحصل على

أ * = .

أ * =

ثم نتبادل الصفين الثاني والثالث من هذه المصفوفة ، ونقسم الصف الثاني من المصفوفة المتغيرة على 2.3333 ، وبالمثل أعلاه ، نضبط المعامِلات في العمود الثاني من الصفين الثالث والرابع من المصفوفة على صفر. يحصل

أ * = .

بعد تنفيذ إجراءات مماثلة في الصفين الثالث والرابع من المصفوفة ، نحصل عليها

أ * = .

بتقسيم الصف الرابع الآن على -5.3076 ، ننتهي من رسم المصفوفة الممتدة للنظام إلى شكل قطري. يحصل

أرز. 2.1. خوارزمية لحل أنظمة المعادلات الجبرية الخطية بطريقة جاوس

أرز. 2.1 أ. ماكروبلوك"حساب قيم الحل".

أ * = .

من السطر الأخير نحصل عليه على الفور x 4 = 0.7536. نتسلق صفوف المصفوفة الآن ونقوم بإجراء الحسابات ، نحصل عليها على التوالي x 3 = 0.7971, x 2 =- 0.1015 و x 1 = 0.3333. بمقارنة الحل الذي تم الحصول عليه بهذه الطريقة مع الحل الذي تم الحصول عليه بواسطة طريقة كرامر ، من السهل التحقق من تطابقهما.

طريقة جاوس جوردان. تشبه طريقة حل SLAE هذه من نواح كثيرة طريقة Gauss. الاختلاف الرئيسي هو أنه باستخدام التحويلات المكافئة ، يتم تقليل المصفوفة الممتدة لنظام المعادلات ليس إلى شكل مثلث ، ولكن إلى شكل قطري ، على القطر الرئيسي الذي توجد فيه وحدات ، وخارجه (باستثناء الأخير ن +1 أعمدة) - أصفار. بعد الانتهاء من هذا التحويل ، سيحتوي العمود الأخير من المصفوفة الموسعة على حل SLAE الأصلي (أي. س ط = أ أنا ن +1 (أنا = 1, 2, … , ن ) في المصفوفة الناتجة). الحركة العكسية (كما في طريقة Gauss) للحسابات النهائية لقيم مكونات الحل ليست ضرورية.

يتم تقليل المصفوفة إلى شكل قطري ، بشكل أساسي ، وكذلك في طريقة Gauss. إذا في الخط أنا معامل في س ط (أنا = 1, 2, … , ن ) صغير في القيمة المطلقة ، ثم يتم البحث عن السلسلة ي ، حيث المعامل عند س ط سيكون أكبر قيمة مطلقة هذا ( ي -i) تم إضافة السلسلة عنصرًا عنصرًا إلى عنصر أنا - الخط ال. ثم كل العناصر أنا - الصف العاشر مقسومًا على قيمة العنصر س ط ولكن ، على عكس طريقة غاوس ، يوجد بعد ذلك عملية طرح من كل سطر برقم ي سطور مع رقم أنا مضروبا أ جي ولكن الشرط ي > أنا طريقة غاوس جوردان تطرح من كل سطر برقم ي , و ي # أنا , سطور مع رقم أنا مضروبا أ جي . هؤلاء. تتم إعادة تعيين المعاملات أسفل القطر الرئيسي وفوقه.

يتم عرض خوارزمية مفصلة إلى حد ما لحل SLAE بطريقة Gauss-Jordan في الشكل. 2.2.

مثال 3. ابحث عن حل SLAE نفسه بطريقة Gauss-Jordan ، والتي حللناها بالفعل بواسطة طرق Cramer و Gauss.

بشكل مشابه تمامًا لطريقة Gauss ، نقوم بتكوين المصفوفة الممتدة للنظام. ثم نتبادل الصفين الأول والثالث من هذه المصفوفة (حيث أن العمود الأول يحتوي على أكبر عنصر قيمة مطلقة) ، ثم نقسم جميع عناصر هذا الصف الأول الجديد على القيمة 3. بعد ذلك ، نطرح من كل صف من الصفوف. المصفوفة (ما عدا الأول) مضروبة عناصر الصف الأول في المعامل في العمود الأول من ذلك الصف. نحصل على نفس طريقة Gauss

أ * = .

ثم نتبادل الصفين الثاني والثالث من هذه المصفوفة ، ونقسم الصف الثاني من المصفوفة المعاد ترتيبها على 2.3333 و ( بالفعل على النقيض من طريقة جاوس) اضبط المعاملات في العمود الثاني من الصفوف الأول والثالث والرابع من المصفوفة على صفر. يحصل

مثال 1. ابحث عن حل عام وبعض الحلول الخاصة للنظام

قرارافعل ذلك باستخدام الآلة الحاسبة. نكتب المصفوفات الموسعة والرئيسية:

يفصل الخط المنقط المصفوفة الرئيسية أ. نكتب الأنظمة المجهولة من أعلى ، مع الأخذ في الاعتبار إمكانية التقليب للمصطلحات في معادلات النظام. عند تحديد رتبة المصفوفة الممتدة ، نجد في نفس الوقت رتبة المصفوفة الرئيسية. في المصفوفة B ، يتناسب العمودان الأول والثاني. من بين العمودين المتناسبين ، يمكن لعمود واحد فقط أن يقع في العمود الثانوي الأساسي ، لذلك دعونا ننتقل ، على سبيل المثال ، العمود الأول بعد الخط المتقطع مع الإشارة المعاكسة. بالنسبة للنظام ، هذا يعني نقل المصطلحات من x 1 إلى الجانب الأيمن من المعادلات.

نحضر المصفوفة إلى شكل مثلث. سنعمل فقط مع الصفوف ، لأن ضرب صف مصفوفة في رقم غير صفري وإضافته إلى صف آخر للنظام يعني ضرب المعادلة بنفس الرقم وإضافتها إلى معادلة أخرى ، وهذا لا يغير الحل النظام. العمل مع الصف الأول: اضرب الصف الأول من المصفوفة في (-3) وأضف الصف الثاني والثالث على التوالي. ثم نضرب الصف الأول في (-2) ونضيفه إلى الصف الرابع.

الخطان الثاني والثالث متناسبان ، لذلك يمكن شطب أحدهما ، على سبيل المثال الثاني. هذا يعادل حذف المعادلة الثانية للنظام ، لأنها نتيجة للمعادلة الثالثة.

الآن نعمل مع السطر الثاني: اضربه في (-1) وأضفه إلى السطر الثالث.

القاصر المتقطع لديه الترتيب الأعلى (من بين جميع القاصرين المحتملين) وهو ليس صفريًا (يساوي حاصل ضرب العناصر على القطر الرئيسي) ، وينتمي هذا القاصر إلى كل من المصفوفة الرئيسية والمصفوفة الممتدة ، وبالتالي النطاق أ = رانج ب = 3.
صغير أساسي. يتضمن معاملات غير معروف x 2 و x 3 و x 4 ، مما يعني أن المجهول x 2 و x 3 و x 4 تابعين و x 1 و x 5 مجانيان.
نقوم بتحويل المصفوفة ، مع ترك العنصر الثانوي الأساسي فقط على اليسار (والذي يتوافق مع النقطة 4 من خوارزمية الحل أعلاه).

النظام الذي يحتوي على معاملات هذه المصفوفة يكافئ النظام الأصلي وله الشكل

بطريقة القضاء على المجهول نجد:
× 4 = 3-4 × 5 ، × 3 = 3-4 × 5 - 2 × 4 = 3-4 × 5 -6 + 8 × 5 = -3 + 4 × 5
س 2 = س 3 + 2 س 4 -2 + 2 س 1 + 3 س 5 = -3 + 4 س 5 + 6-8 س 5 -2 + 2 س 1 + 3 س 5 = 1 + 2 س 1-س 5
لدينا علاقات تعبر عن المتغيرات التابعة x 2 ، x 3 ، x 4 خلال x 1 و x 5 ، أي أننا وجدنا حلًا عامًا:

بإعطاء قيم عشوائية للمجهول المجاني ، نحصل على أي عدد من الحلول الخاصة. لنجد حلين معينين:
1) دع x 1 = x 5 = 0 ، ثم x 2 = 1 ، x 3 = -3 ، x 4 = 3 ؛
2) ضع x 1 = 1 ، x 5 = -1 ، ثم x 2 = 4 ، x 3 = -7 ، x 4 = 7.
وهكذا وجدنا حلين: (0.1 ، -3 ، 3 ، 0) - حل واحد ، (1.4 ، -7.7 ، -1) - حل آخر.

مثال 2. تحقق من التوافق ، وابحث عن حل عام وآخر خاص للنظام

قرار. دعونا نعيد ترتيب المعادلتين الأولى والثانية للحصول على وحدة في المعادلة الأولى وكتابة المصفوفة ب.

نحصل على الأصفار في العمود الرابع ، تعمل في الصف الأول:

احصل الآن على الأصفار في العمود الثالث باستخدام الصف الثاني:

الصفان الثالث والرابع متناسبان ، لذا يمكن شطب أحدهما دون تغيير الترتيب:
اضرب الصف الثالث في (-2) وأضف إلى الرابع:

نرى أن رتب المصفوفات الرئيسية والممتدة هي 4 ، وتتزامن الرتبة مع عدد المجهول ، لذلك فإن النظام لديه حل فريد:
-x 1 \ u003d -3 → x 1 \ u003d 3 ؛ × 2 \ u003d 3-× 1 → × 2 \ u003d 0 ؛ × 3 \ u003d 1-2x 1 → × 3 \ u003d 5.
× 4 \ u003d 10-3x 1-3x 2-2x 3 \ u003d 11.

مثال 3. افحص النظام للتأكد من توافقه وابحث عن حل إذا كان موجودًا.

قرار. نقوم بتكوين المصفوفة الممتدة للنظام.

أعد ترتيب المعادلتين الأوليين بحيث يكون هناك 1 في الزاوية اليسرى العليا:
بضرب الصف الأول في (-1) ، نضيفه إلى الصف الثالث:

اضرب السطر الثاني في (-2) وأضف إلى السطر الثالث:

النظام غير متسق ، لأن المصفوفة الرئيسية تلقت صفًا يتكون من أصفار ، يتم شطبها عند العثور على الرتبة ، ويظل الصف الأخير في المصفوفة الممتدة ، أي r B> r A.

يمارس. تحقق من نظام المعادلات هذا من أجل التوافق وحلها عن طريق حساب المصفوفة.
قرار

مثال. إثبات توافق نظام المعادلات الخطية وحلها بطريقتين: 1) بطريقة غاوس. 2) طريقة كرامر. (أدخل الإجابة بالصيغة: x1 ، x2 ، x3)
الحل: doc: doc: xls
إجابه: 2,-1,3.

مثال. نظام المعادلات الخطية معطى. إثبات توافقها. ابحث عن حل عام للنظام وحل معين واحد.
قرار
إجابه:× 3 \ u003d - 1 + × 4 + × 5 ؛ × 2 \ u003d 1 - × 4 ؛ س 1 = 2 + س 4 - 3 س 5

يمارس. ابحث عن حلول عامة وخاصة لكل نظام.
قرار.ندرس هذا النظام باستخدام نظرية Kronecker-Capelli.
نكتب المصفوفات الموسعة والرئيسية:

1	1	14	0	2	0
3	4	2	3	0	1
2	3	-3	3	-2	1
× 1	x2	× 3	x4	x5

هنا المصفوفة A بخط عريض.
نحضر المصفوفة إلى شكل مثلث. سنعمل فقط مع الصفوف ، لأن ضرب صف مصفوفة في رقم غير صفري وإضافته إلى صف آخر للنظام يعني ضرب المعادلة بنفس الرقم وإضافتها إلى معادلة أخرى ، وهذا لا يغير الحل النظام.
اضرب الصف الأول ب (3). اضرب الصف الثاني في (-1). دعنا نضيف السطر الثاني إلى السطر الأول:

0	-1	40	-3	6	-1
3	4	2	3	0	1
2	3	-3	3	-2	1

اضرب الصف الثاني ب (2). اضرب الصف الثالث في (-3). دعنا نضيف السطر الثالث إلى السطر الثاني:

0	-1	40	-3	6	-1
0	-1	13	-3	6	-1
2	3	-3	3	-2	1

اضرب الصف الثاني في (-1). دعنا نضيف السطر الثاني إلى السطر الأول:

0	0	27	0	0	0
0	-1	13	-3	6	-1
2	3	-3	3	-2	1

القاصر المختار له أعلى رتبة (من بين جميع القاصرين المحتملين) ويختلف عن الصفر (يساوي حاصل ضرب العناصر على المائل المقلوب) ، وينتمي هذا القاصر إلى كل من المصفوفة الرئيسية والمصفوفة الممتدة ، وبالتالي النطاق (أ) = رانج (ب) = 3 بما أن مرتبة المصفوفة الرئيسية تساوي مرتبة المصفوفة الممتدة ، إذن النظام تعاوني.
هذا القاصر أساسي. يتضمن معاملات للمجهول x 1 ، x 2 ، x 3 ، مما يعني أن المجهول x 1 ، x 2 ، x 3 تابع (أساسي) ، و x 4 ، x 5 مجاني.
نقوم بتحويل المصفوفة ، مع ترك الصغرى الأساسية فقط على اليسار.

0	0	27	0	0	0
0	-1	13	-1	3	-6
2	3	-3	1	-3	2
× 1	x2	× 3		x4	x5

النظام الذي يحتوي على معاملات هذه المصفوفة يكافئ النظام الأصلي وله الشكل:
27 × 3 =
- x 2 + 13x 3 = - 1 + 3x 4-6x 5
2 س 1 + 3 س 2 - 3 س 3 = 1 - 3 س 4 + 2 س 5
بطريقة القضاء على المجهول نجد:
حصلنا على العلاقات التي تعبر عن المتغيرات التابعة x 1 ، x 2 ، x 3 حتى x 4 ، x 5 ، أي أننا وجدنا قرار مشترك:
× 3 = 0
س 2 = 1 - 3 × 4 + 6 × 5
س 1 = - 1 + 3 س 4-8 س 5
غير مؤكد، لان لديه أكثر من حل.

يمارس. حل نظام المعادلات.
إجابه: × 2 = 2 - 1.67 × 3 + 0.67 × 4
× 1 = 5 - 3.67 × 3 + 0.67 × 4
بإعطاء قيم عشوائية للمجهول المجاني ، نحصل على أي عدد من الحلول الخاصة. النظام غير مؤكد

شكل المصفوفة

يمكن تمثيل نظام المعادلات الخطية في شكل مصفوفة على النحو التالي:

أو وفقًا لقاعدة ضرب المصفوفات ،

أX = ب.

إذا تمت إضافة عمود من المصطلحات المجانية إلى المصفوفة A ، فإن A تسمى المصفوفة المعززة.

طرق الحل

تسمح لك الطرق المباشرة (أو الدقيقة) بالعثور على حل في عدد معين من الخطوات. تعتمد الطرق التكرارية على استخدام عملية متكررة وتسمح لك بالحصول على حل كنتيجة للتقديرات المتتالية

الطرق المباشرة

• طريقة المسح (للمصفوفات ثلاثية الأضلاع)
• تحلل تشوليسكي أو طريقة الجذر التربيعي (لمصفوفات متماثلة موجبة ومصفوفات هرميتية)

الطرق التكرارية

حل نظام المعادلات الجبرية الخطية في VBA

خيار إعادة تعبئة فرعية صريحة () Dim i As Integer Dim j As Integer Dim r () as double Dim p as double Dim x () as double Dim k as Integer Dim n as Integer Dim b () as double Dim file as Integer Dim y () كملف مزدوج = FreeFile فتح "C: \ data.txt" للإدخال كملف إدخال # ملف ، n ReDim x (0 إلى n * n - 1) كـ Double ReDim y (0 إلى n - 1) كـ Double ReDim r (0 إلى n - 1) كمزدوجة لـ i = 0 إلى n - 1 بالنسبة إلى j = 0 إلى n - 1 Input #file، x (i * n + j) التالي j Input #file، y (i) التالي i أغلق #file لـ i = 0 إلى n - 1 p = x (i * n + i) بالنسبة لـ j = 1 إلى n - 1 x (i * n + j) = x (i * n + j) / p التالي j y (i) = y (i) / p بالنسبة إلى j = i + 1 إلى n - 1 p = x (j * n + i) بالنسبة إلى k = i إلى n - 1 x (j * n + k) = x (j * n + k) - x (i * n + k) * p التالي k y (j) = y (j) - y (i) * p التالي j التالي i "مصفوفة مثلثة عليابالنسبة إلى i = n - 1 إلى 0 الخطوة -1 p = y (i) بالنسبة إلى j = i + 1 إلى n - 1 p = p - x (i * n + j) * r (j) التالي j r (i) = p / x (i * n + i) التالي i "Backtrack For i = 0 To n - 1 MsgBox r (i) Next i"نهاية الفرعية

أنظر أيضا

الروابط

ملاحظات

مؤسسة ويكيميديا. 2010.

شاهد ما هو "SLAU" في القواميس الأخرى:

SLAU- نظام المعادلات الجبرية الخطية ... قاموس الاختصارات والاختصارات

هذا المصطلح له معاني أخرى ، انظر سلو (معاني). المدينة والوحدة الوحدوية في Slough Engl. سلو كونتري ... ويكيبيديا

- (سلو) مدينة في المملكة المتحدة ، وهي جزء من الحزام الصناعي المحيط بلندن الكبرى ، في سكة حديديةلندن بريستول. 101.8 ألف نسمة (1974). الهندسة الميكانيكية والكهربائية والإلكترونية والسيارات والكيميائية ... ... الموسوعة السوفيتية العظمى

سلو- (سلو) سلاو ، مدينة صناعية وتجارية في بيركشاير جنوبا. إنجلترا ، غرب لندن ؛ 97400 نسمة (1981) ؛ بدأت الصناعة الخفيفة تتطور في الفترة ما بين الحربين العالميتين ... دول العالم. كلمات

سلو: سلو هي مدينة في إنجلترا ، في مقاطعة بيركشاير SLAU نظام المعادلات الجبرية الخطية ... ويكيبيديا

كومونة روسلاو روسلاو شعار النبالة ... ويكيبيديا

مدينة باد فوسلاو باد فوسلاو شعار النبالة ... ويكيبيديا

تعد طرق الإسقاط لحل SLAE فئة من الأساليب التكرارية يتم فيها حل مشكلة إسقاط متجه غير معروف على مساحة معينة على النحو الأمثل فيما يتعلق ببعض المساحة الأخرى. المحتويات 1 بيان المشكلة ... ويكيبيديا

مدينة باد فوسلاو باد فوسلاو البلد النمساالنمسا ... ويكيبيديا

النظام الأساسي للحلول (FSR) عبارة عن مجموعة من الحلول المستقلة خطيًا لنظام متجانس من المعادلات. المحتويات 1 الأنظمة المتجانسة 1.1 مثال 2 أنظمة غير متجانسة ... ويكيبيديا

كتب

• المشاكل المباشرة والعكسية لإعادة بناء الصورة والتحليل الطيفي والتصوير المقطعي باستخدام MatLab (+ CD) ، سيزيكوف فاليري سيرجيفيتش. يصف الكتاب استخدام جهاز المعادلات المتكاملة (IU) وأنظمة المعادلات الجبرية الخطية (SLAE) وأنظمة المعادلات الخطية غير الخطية (SLNU) ، وكذلك أدوات البرمجيات ...