Определение поддържащи реакциигреди
Върху опорите на гредата възникват реакции, с определянето на които трябва да се започне решаването на всички проблеми на изчисляването на огъване.
Реакциите на опорите се определят от уравненията на равновесието (статиката), които могат да бъдат представени в два различни варианта:
1) под формата на сбора от проекциите на всички сили върху оста хи в, както и сумата от моментите на силите (включително реакциите) спрямо всяка точка по оста на гредата:
Равновесните уравнения са много важни, когато става въпрос за анализ на лъча. Използвайки тези три уравнения, можете да откриете неизвестните стойности за отговорите на подкрепа, като знаете силните страни и дължините на сегментите на гредата. Моментното уравнение е наистина полезно, защото ви позволява да решите проблема, без да разлагате определени сили, всяка сила, действаща на същата права, която приемате в момента, е нула.
Така че, ако имате три неизвестни сили, но 2 от тях преминават през една и съща точка, тогава вземането на момента в този момент ще пренебрегне тези сили и ще изолира третата страна в разрешимото уравнение. Стъпка 5 Решете вътрешната аксиална сила на разреза, като сумирате всички сили, успоредни на гредата. Стъпка 6 Решете вътрешната сила на срязване на срязаната секция, като сумирате всички сили, перпендикулярни на гредата. Стъпка 7 Решете силата на вътрешния момент на разреза, като сумирате външните моменти на сила, както и всички точкови моменти на среза.
2) като сбор от всички сили върху една от координатните оси хили ви две суми от моменти на силите (включително реакции) около две точки, лежащи върху оста на гредата:
Изборът на един или друг вариант за съставяне на уравнения на равновесие, както и изборът на точки по посоката на координатните оси, използвани при съставянето на тези уравнения, се извършва във всеки конкретен случай по такъв начин, че по възможност да се получи съвместно решение на уравненията не се изпълнява. За да се провери правилността на определяне на опорните реакции, се препоръчва да се заменят техните стойности във всяко равновесно уравнение, което не е било използвано преди.
Построяване на диаграми на срязване и моменти
Стъпка 8 Ако искате да тествате вашите решения за вътрешна сила, използвайте изоставения разрез в стъпка 4 и изчислете вътрешни силив стъпки 5-7. Трябва да получите същия отговор. Следващите стъпки представят графичен метод за конструиране на диаграми на срязване и моменти.
Стъпка 1 Начертайте диаграма на тялото без лъчи и посочете конвенция, която ще се използва в цялото решение. Стъпка 2 Решете всички неизвестни външни реакции, като използвате трите равновесни уравнения. Стъпка 3 След като изчислите всички външни реакции, можете да продължите към диаграмата на смяната. Погледнете диаграмата на свободното тяло, започвайки от лявата страна на гредата. Ако няма натоварване в края, можете да продължите към следващата стъпка, тъй като изместването в точката е нула. Въпреки това, ако има разположена сила, тогава линията може да бъде изтеглена от нула до величината на концентрирания товар.
При определяне на реакциите техните посоки могат да се избират произволно. Ако реакциите в изчислението се оказаха отрицателни, това означава, че тяхната посока е избрана неправилно. В този случай на изчислителна схеманачалната посока на реакциите е зачертана и е посочена обратната им посока. При последващи изчисления стойностите на реакцията се приемат за положителни.
Посоката на точката зависи от това дали силата е положителна или отрицателна. Стъпка 4 Сега продължете да гледате вдясно от гредата, докато чертаете хоризонтална линия, докато се покаже друга стойност за натоварването, ако това е друго точково натоварване, тогава ще продължите от точката, която сте спрели в предишния раздел и можете да добавите или извадете стойностна сила в зависимост от нейната посока. В крайна сметка ще направите това, докато стигнете до другата страна на лъча. Ако имаше равномерно разпределен товар върху гредата, в зависимост от дължината на разпределението, линията ще бъде начертана диагонално, свързвайки положителните и отрицателните стойности на площта разпределен товар.
Възможно е обаче предварително да се предвиди правилната посока на реакциите въз основа на мислено представената еластична линия на гредата, след като тя бъде натоварена от външни сили (фиг. НО) реакция Р Аима посока към опората; при "натискане" на гредата в опората (подпора AT) реакция Р Бима посока далеч от опората.
Докато стигнете до десния край на лъча, диаграмата трябва да се върне на нула. Стъпка 5 Добре е да се отбележи, че всяка линия, която пресича оста, за да премине от положителна към отрицателна, трябва да се има предвид, когато се чертае моментната диаграма, тъй като тя става максимална или минимална стойност, когато наклонът е в нулева точка. Стъпка 6 За да начертаете моментна диаграма, първо трябва да проверите левия край на лъча, за да видите дали има някакъв момент във времето. Ако е така, ще има скок от нула до стойността на точковото натоварване.

Фигура 8.5 - За определяне на посоката на реакциите
Помислете за типични случаи на определяне на реакции за най-простите видове товари.
Ако върху лъча се въздейства от интензитета q, както е показано на фиг. 8.6, то при определяне на опорните реакции натоварването се заменя с неговия резултат Р, равно на произведението от интензивността на натоварването qза дължината на зоната му на действие л
Ако нямаше моментен момент за безплатна диаграма на тялото, щяхте да започнете диаграмата си от нулата. Стъпка 7 Площта под диаграмата на срязване е наклонът на момента на моментната диаграма. Така че, за да стане просто, разделете диаграмата на срязване на общи цифрии изчислете площта на всеки от тях и стойността, която получавате, може да бъде нанесена на диаграмата на момента. Ще направите това, като се придвижите към дясната страна на лъча.
Също така начертайте диаграма на срязване и момент за гредата, както е показано по-долу. Диаграмата на срязване и момент за Пример 1 е показана по-долу. Забележка. Можете да проверите дали отговорът ви е правилен или не, като сравните стойностите на смяната, получени при метода на изрязване, със стойностите на диаграмата на смяна, ако и двете стойности са равни, тогава решението е правилно и без грешки.
Пример за непрекъснат равномерно разпределен товар е собственото тегло на гредата или често разположените товари по дължината й.

Фигура 8.6 - Случаят на равномерно разпределен товар върху гредата
Точка на приложение на непрекъснат равномерно разпределен товар qлежи в средата на зоната, върху която действа; с триъгълен закон на действие на разпределения товар, резултатът се прилага по центъра на тежестта му.
Пример 2. Дефинирайте уравненията за аксиална сила, сила на срязване и огъващ момент като функция на положението по дължината на гредата. Начертайте диаграма на силата на срязване и диаграма на момента на огъване за гредата по-долу на фигурата. След това определете неизвестните сили за всеки разрез, като използвате 3-те уравнения на равновесие.
Търсене на реакции на непрекъснати лъчи. Изолирайте всеки участък на гредата и считайте всеки един от тях за просто поддържан, като поддържате първоначалното натоварване на участъка и изчислените крайни моменти. Нека разбием още един участък на прости греди, едната от които носи дадените натоварвания плюс другата греда, която носи крайните моменти и реакциите на двойката. С този метод вътрешната реакция беше разделена на части, които могат да бъдат сумирани, за да се намери пълната реакция.
Размер на интензивността на натоварването qобикновено се изразява в kN/m или kN/cm.
Помислете за последователността на определяне на опорните реакции в случай на натоварване на гредата, показана на фиг. 8.7:
1. Приетата посока на реакциите е показана на проектната диаграма на гредата Р Аи Р Бвъзникващи върху подпорите. Тъй като външното натоварване действа във вертикална равнина, перпендикулярна на оста на гредата, хоризонталната реакция върху шарнирната опора НОотсъства.
Задача 828 - Непрекъснати реакции на лъча
Общи указания В следващите задачи идентифицирайте реакциите и начертайте диаграми на смяна. При решаване на задачи използвайте точките, посочени в контролните задачи, освен ако не е посочено друго. Непрекъсната греда носи равномерно натоварване в две равни пространства, както е показано на фиг.
По този начин можете да съкратите решението, без да правите всички изчисления, свързани с втория интервал. Диаграмите на гредата се използват като основен начин за обучение на инженерите за основно статично натоварване. Гредите са конструктивни елементи, които могат да издържат на натоварване поради своята устойчивост на огъване. Силата на огъване може да бъде резултат от външни натоварвания, тегло или дължина на гредата. Поради тези натоварвания гредите изпитват момент на огъване и момент на срязване.
2. Тъй като в този случай има две неизвестни реакции ( Р Аи Р Б), тогава две уравнения се вземат като равновесни за определяне на реакциите
При съставянето на тези условия на равновесие трябва да се приеме правилото за знаците за моментите на силите, включително реакциите. Обикновено такова правило се приема за външни (активни) знаци: ако моментите от силите са насочени по посока на часовниковата стрелка, тогава те се считат за положителни.
Гредите се класифицират въз основа на техните опори. В допълнение към гредите, поддържани от ферма, гредите се класифицират в следните групи. Просто поддържан: Гредата се поддържа в краищата, които могат да се въртят свободно и нямат моментално съпротивление. Фиксирана: Гредата от двете страни е фиксирана на място.
Надвес: Проста греда, простираща се отвъд нейната опора в единия край. Двоен надвес: Проста греда с двата края, излизащи извън нейните опори. Непрекъснато: Греда, обхващаща повече от две опори. Конзола: Проекционният лъч е фиксиран само в единия край, а другият край не се поддържа.
Тогава първото условие на равновесие (8.4) води до уравнението за неизвестната реакция Р Б(виж фиг.8.6)
![]()
![]()
Реакцията се оказа положителна, поради което посоката й беше приета за правилна.
По-долу ще анализираме някои класически примери за натоварване на тези категории греди. Една проста греда има две опори във всеки край. Тези опори или реакции не са фиксирани, така че са свободни да се движат. Това влияе върху това как натоварванията ще реагират на опорите по отношение на срязващия и огъващ момент. Ако бъдат коригирани, силите на срязване и моментите биха реагирали по различен начин. Първият случай е концентриран товар, който действа върху гредата в нейния център. Величината на силата за всяка реакция е равна на натоварването в центъра.
В случай на концентриран товар в центъра напрежението на срязване има същата стойност като реакционната сила. Създава се диаграма на срязване, като се анализират силите, действащи върху греда от едната страна на другата. Ако започнем от лявата страна, силите на реакцията ще започнат да се издигат нагоре по гредата. Това кара моделът на срязване да се повиши до същата стойност и да не се пресича, докато не достигне централното натоварване. След това стойността на срязване се насочва към същата стойност като централното натоварване и продължава без наклон, докато достигне второто реакционно натоварване в другия край на гредата.
По същия начин използваме второто условие на равновесие (8.4), което води до уравнението за втората реакция Р А:
![]()
![]()
Отново реакцията се оказа положителна, следователно първоначалната й посока в изчислителната схема е избрана правилно.
Моментът се определя по същия начин. Наклонът на моментната диаграма в интервал 0 е равен на стойността на изместването. Промяната в момента е равна на площта под диаграмата на срязване. В този случай максималният въртящ момент се определя от следното уравнение. Стойностите на отговора ще бъдат определени. Използвайки уравненията за реакционно натоварване по-горе, можете да модифицирате предишните формули, ако е необходимо.

Другият случай на натоварване е единичен товар. Натоварването се разпределя равномерно по дължината на гредата. Разпределеният товар се определя количествено като товар на разстояние и може също да бъде приравнен на концентриран товар в определена точка по протежение на прът. Големината на силата е равна на площта под кривата на разпределения товар, а местоположението е в центъра на масата на разпределения товар. За този случай се изразява силата на реакция, която е и максималната сила на срязване.
3. Проверяваме правилността на определяне на величините на реакциите, като използваме друго, неизползвано преди, условие на равновесие
В този случай проекциите на силите съвпадат с посоката на оста в, се считат за положителни, а насочени в обратна посока – отрицателни.
Тогава, въз основа на използването на условие (8.5), имаме:
Тук диаграмата на срязване и диаграмата на моментите се променят леко. В първия случай моделът на срязване върви направо, докато удари товар и се премести обратната страна. Изместването във втория случай е непрекъснат отрицателен наклон. За да намерите силата на срязване във всяка точка, използвайте уравнението.
Максималният момент може да бъде определен. 
За фиксиран лъч разликата ще бъде видима на диаграмата на моментите. Реакционните сили са същите като при обикновен лъч. Диаграмата на срязване също ще се държи така, както беше намерена в първия случай на обикновена греда. Сега обаче, когато краищата са фиксирани, моментът в опорите ще бъде постигнат по различен начин. Моментът в центъра и в краищата може да бъде изразен със същото уравнение.
![]()
Получената идентичност (0=0) показва правилността на определянето на стойностите на реакцията при изчисляването на огъването на гредата.
Помислете за друг типичен случай на натоварване под формата на ексцентрично разположена концентрирана сила Рпо дължината на гредата л(фиг.8.7).
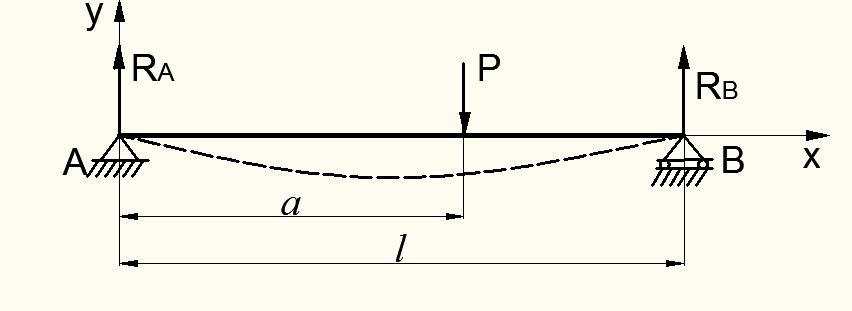

Надвесната греда има първата опора в края на гредата, а втората опора е разположена по протежение на гредата към центъра. В този конкретен пример частта от гредата, която преминава през втората опора, не изпитва срязване или огъване. Визуалното изображение на срязване и огъване е подобно на обикновена греда. Въпреки това, тъй като примерът по-горе няма централно натоварване, изчисленията на срязване ще бъдат различни за всяка опора.
Максималният момент се изчислява по следното уравнение. 
Двойната надвесна греда е същата концепция като единична греда, с изключение на двете опори, разположени по протежение на и вътре по дължината на гредата. В този случай натоварването през гредата е равномерно натоварване и по-ефективно влияе на диаграмите на срязване и огъване. Отляво надясно, първата стойност на срязване се определя от разстоянието на първата опора до края, умножено по равномерното натоварване.
Фигура 8.7 - Случаят на натоварване на греда с концентрирана сила
1. Ще покажем на изчислителната схема на реакцията Р Аи Р Б. Те са насочени, както бе споменато по-горе, към товара.
2. Определяме реакциите от условията на равновесие:
Реакциите се оказаха положителни, следователно първоначалната им посока в изчислителната схема е избрана правилно.
Имайте предвид в същото време, че реакцията на подкрепата ATсе оказа повече от реакцията на поддръжката НО: R B ˃R A. Това следва от факта, че властта Ре по-близо до основата AT, и следователно го натоварва повече.
3. Проверете:
Получената идентичност показва правилността на определението на реакцията.
Нека разгледаме още един случай на натоварване на гредата в участък от външен концентриран момент (фиг. 8.8), който се осъществява при практически изчисления на огъване.
| 𝔐 |

Фигура 8.8 - Случаят на натоварване на гредата с концентриран момент
1. Нека покажем на изчислителната схема очакваната посока на реакциите (отначало не знаем дали тези посоки са взети правилно).
2. Реакциите се определят от уравненията на равновесието:
Реакцията се оказа положителна, следователно първоначалната й позиция е избрана правилно.
Реакцията се оказа отрицателна, което означава, че посоката й е избрана неправилно. Следователно, върху схемата на проектиране, ние зачеркваме първоначално (погрешно) приетата посока Р Аи покажете обратната (истинска) посока (вижте фигура 8.8). При по-нататъшни изчисления разглеждаме реакцията Р Ас правилната посока на положителното.
3. Проверете:
Уравнението на равновесието, използвано за лъча, е изпълнено, което означава, че реакциите и тяхната посока са определени правилно.
Ако една греда при напречно огъване има такива опори, че общият брой на реакциите, протичащи върху опорите, не надвишава две, тогава реакциите винаги могат да бъдат определени от две уравнения на равновесие от типа (8.2). Такива греди, чиито реакции се определят от тези статични уравнения, се наричат статично детерминирангреди. Тези греди могат да бъдат от най-простите видове (фиг. 8.9):
Фигура 8.9 - Статично дефинирани греди
1) греда с един твърдо захванат, а другият свободен край, в противен случай конзола(фиг.8.9, а); 2) шарнирни греди (фиг. 8.9, би 8.9, в).
Греди, в които общият брой на опорните реакции е по-голям от броя на уравненията на равновесието, се наричат статично неопределени(изчисляването на тяхното огъване ще бъде разгледано в раздел 8.10). За такива греди реакциите на опорите се определят от съвместното решение на уравненията на статиката и условията за съвместимост на деформациите.
Свободният прът, разгледан в § 2.7, беше натоварен с дадени натоварвания (сили и моменти) в равновесие (виж фиг. 3.7). Обикновено дадените натоварвания не са взаимно балансирани; неподвижността на конструкцията под действието на тези натоварвания се осигурява от наличието на опори, свързващи я с основата. В опорите възникват реакции, които заедно с дадените натоварвания представляват балансирана система от външни сили, действащи върху конструкцията.
Както е известно от курса теоретична механика, всяко тяло има три степени на свобода в равнината. Следователно, за да се осигури геометричната неизменност на системата (лъча), е необходимо да се наложат три ограничения върху нея (в равнината).
Обмисли Различни видовеопори на плоски системи.
1. Прищипване или запечатване (фиг. 4.7, а). Прищипаният (или вграденият) край на гредата не може нито да се движи напред, нито да се върти. Следователно, броят на степените на свобода на лъч с прищипан крайравно на нула. В опората може да възникне следното: вертикална реакция (сила R - фиг. 4.7, а), която предотвратява вертикалното изместване на края на гредата; хоризонтална реакция (сила N), изключваща възможността за нейното хоризонтално изместване и реактивния момент, предотвратяващ въртенето. По този начин фиксирането на гредата с помощта на вграждане налага три връзки върху нея и гарантира нейната неподвижност.
2. Шарнирна фиксирана опора (фиг. 4.7, б). Напречното сечение на гредата, преминаваща през шарнирно фиксираната опора, не може да бъде преместено напред. В опората възниква реактивна сила, преминаваща през центъра на пантата. Неговите компоненти са вертикалната сила R, която предотвратява вертикалното изместване, и хоризонталната сила H, която изключва хоризонталното изместване на фиксирания участък на гредата. Опората не пречи на гредата да се завърти спрямо центъра на пантата и следователно гредата, фиксирана с една такава опора, има една степен на свобода. Фиксирането на гредата с помощта на шарнирно фиксирана опора налага две връзки върху нея.
3. Шарнирна подвижна опора (фиг. 4.7, в). Напречното сечение на гредата, преминаваща през шарнирно подвижната опора, може да се измести успоредно на опорната равнина и да се завърти, но не може да бъде изместено перпендикулярно на опорната равнина. В опората протича само една реакция под формата на сила R, перпендикулярна на равнината на опората. Фиксирането на греда с такава опора налага една връзка върху нея.
Разгледаните видове опори също обикновено се изобразяват с помощта на пръти.
Шарнирно подвижна опора е изобразена под формата на прът с панти в краищата (фиг. 5.7, а). Долната панта е фиксирана, а горната може да се движи само по права линия, перпендикулярна на оста на пръта.

Това съответства на условията на фиксиране, осигурени от шарнирно подвижната опора (виж фиг. 4.7, c). Опорната реакция действа само по оста на пръта. Неговите собствени деформации не се вземат предвид при изчисленията, т.е. пръчката се счита за безкрайно твърда.
Съчленена неподвижна опора е изобразена с помощта на два пръта с панти в краищата (фиг. 5.7, б). Горната панта е обща и за двата пръта. Посоките на прътите могат да бъдат произволни. Те обаче не трябва да са разположени на една и съща права линия.
Уплътнението (прищипване) може да бъде изобразено с помощта на три пръта с панти в краищата, както е показано на фиг. 5.7, c.
Брой пръчки в схематично представянеопората е равна на броя на компонентите на опорната реакция и броя на връзките, наложени от тази опора върху структурата.
За да не се движи гредата под натоварване, тя трябва да бъде геометрично неизменно (фиксирана) свързана с основата, което в случай на плоско действие на силите, както вече беше отбелязано, се постига чрез налагане на три външни връзки върху нея.

Това може да стане с помощта на едно уплътнение (фиг. 6.7, а) или една шарнирно фиксирана и една шарнирно подвижна опора (фиг. 6.7, б), или с помощта на три шарнирно подвижни опори, чиито посоки на реакция не се пресичат в една точка ( Фиг. 6.7, c).

Ако посоките на трите опорни пръта се пресичат в една точка O (фиг. 7.7, a, b), тогава системата е моментално променлива, тъй като в този случай нито един поддържащ прът не предотвратява много малко завъртане на гредата около точката О; такова разположение на опорните пръти е неприемливо.
Помислете за геометрично неизменни системи, състоящи се от няколко пръта.

На фиг. 8.7 и, например, е показана система от две ленти (AB и BC), всяка от които има три връзки. Една връзка е наложена върху гредата BC от носещия прът CD, който предотвратява вертикалното изместване на точка C на гредата, и две връзки - пантата B, която предотвратява вертикалното и хоризонталното изместване на точка B на гредата.
Върху гредата AB и трите връзки се прилагат чрез уплътнение A; пантата B не може да предотврати транслационни измествания или завъртания на греда AB и следователно не налага ограничения върху нея.
На фиг. 8.7, b показва геометрично неизменна система, състояща се от три ленти (AC, CD и DF). Всеки от тях има три връзки. Така, например, пантата C налага две връзки върху лентата CD (защото предотвратява хоризонтално и вертикално изместване на точка C), а пантата - една връзка (тъй като предотвратява само вертикалното изместване на точката).
Системите, изобразени на фиг. 8.7 се наричат многопролетни шарнирни греди.
Общият брой неизвестни опорни реакции за опциите за фиксиране на гредата, показани на фиг. 6.7, a, b, c, е равно на три. Следователно, тези реакции могат да бъдат намерени с помощта на три уравнения на равновесие, които са съставени за плоска система от сили. Според стойностите на опорните реакции и външните натоварвания е възможно да се определят [по формули (2.7) - (4.7)] вътрешни сили във всяко напречно сечение на гредата. Следователно гредата, фиксирана чрез налагане на три връзки върху нея, е не само геометрично неизменна, но и статично определена. Налагането на по-голям брой ограничения върху него прави лъча статично неопределен, тъй като в този случай всички опорни реакции не могат да бъдат определени само от уравненията на равновесието.
Уравненията на равновесието, съставени за определяне на поддържащите реакции, могат да бъдат представени в три различни версии:
1) под формата на суми от проекции на силите върху две произволни оси, които не са успоредни една на друга, и суми от моменти на силите спрямо която и да е точка от равнината на МО);
2) под формата на сбора от проекции на силите върху произволна ос и две суми от моменти спрямо всички точки от равнината, които не лежат върху един и същ перпендикуляр на определената проекционна ос
3) под формата на три суми от моменти за всички точки от равнината, които не лежат на една права линия
Изборът на един или друг вариант за съставяне на уравнения на равновесие, както и изборът на точки и посоки на осите, използвани при съставянето на тези уравнения, се извършва във всеки конкретен случай по такъв начин, че по възможност съвместно решаване на уравненията не се осъществява. За да се провери правилността на определяне на опорните реакции, се препоръчва да се заменят техните стойности във всяко равновесно уравнение, което не е било използвано преди.
На много участък шарнирна гредапоказано на фиг. 8.7, а, четири външни връзки са насложени (три в секция А и една в секция С), а върху гредата, показана на фиг. 8.7, b, - пет външни връзки (две в секция A и по една в секции B, E и F).
Въпреки това, ако три връзки са наложени на всяка греда, която образува шарнирна греда с няколко участъка, тогава тази греда е статично определена и опорните реакции могат да бъдат намерени от уравненията на статиката.
В допълнение към трите уравнения за баланса на всички сили, действащи върху шарнирна греда с няколко участъка, се съставят уравнения, които изразяват равенството на нула на моментите на силите, приложени от едната страна на всяка панта (свързване на отделни части на гредата) спрямо центъра на тази панта. Например, за лъча, показан на фиг. 8.7, но в допълнение към трите уравнения на равновесието на всички действащи върху него сили се съставя уравнение за моментите на левите (или десните) сили спрямо шарнира и за гредата, показана на фиг. 8.7, b, - по отношение на пантите C и D.

Помислете за пример за определяне на опорните реакции на обикновена греда с един участък, чиято конструктивна схема е показана на фиг. 9.7, а. Изхвърляме опорите и заменяме тяхното влияние върху гредата с опорните реакции RA, H и RB (фиг. 9.7, б). Обикновено греда с изхвърлени опори не се показва отделно, а обозначенията и посоките на реакциите на опората са посочени на проектната диаграма на гредата. Реакциите са вертикалните и хоризонталните компоненти на общата реакция на шарнирно фиксираната опора А; силата е общата реакция на опората B. Посоките на опорните реакции се избират произволно; ако в резултат на изчислението стойността на която и да е реакция се окаже отрицателна, тогава всъщност нейната посока е противоположна на приетата преди.
Нека първо намерим опорната реакция H, като компенсираме за това сумата от проекциите на всички сили върху хоризонталната ос x:
За да проверим намерените стойности на опорните реакции, съставяме сбора от проекциите на всички сили върху оста y.
Формулираното уравнение е изпълнено, което показва коректността на определяне на опорните реакции.