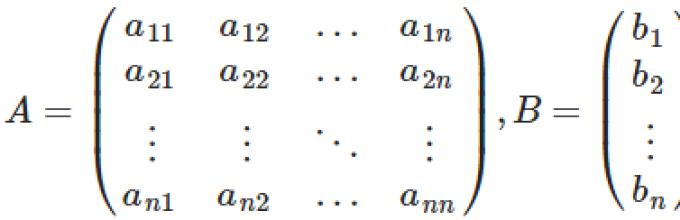Матричен метод SLAU решенияизползва се за решаване на системи от уравнения, в които броят на уравненията съответства на броя на неизвестните. Методът се използва най-добре за решаване на системи от нисък ред. Матричният метод за решаване на системи от линейни уравнения се основава на прилагането на свойствата на матричното умножение.
По този начин, с други думи метод на обратна матрица,наречен така, тъй като решението се свежда до обичайното матрично уравнение, за чието решение трябва да намерите обратната матрица.
Метод на матрично решение SLAE с детерминанта, по-голяма или по-малка от нула, е както следва:
Да предположим, че има SLE (система от линейни уравнения) с ннеизвестно (над произволно поле):
Така че е лесно да го преведете в матрична форма:
AX=B, където Ае основната матрица на системата, Би х- колони със свободни членове и решения на системата, съответно:

Умножете това матрично уравнение вляво по А -1- обратна матрица към матрица A: A −1 (AX)=A −1 B.
Защото A −1 A=E, означава, X=A −1 B. Дясната страна на уравнението дава колона от решения на първоначалната система. Условието за приложимостта на матричния метод е неизродеността на матрицата А. Необходимо и достатъчно условие за това е детерминантата на матрицата А:
detA≠0.
За хомогенна система от линейни уравнения, т.е. ако вектор B=0, изпълнено обратното правило: в системата AX=0е нетривиално (т.е. не е равно на нула) решение само когато detA=0. Тази връзка между решенията на хомогенни и нехомогенни системи от линейни уравнения се нарича алтернатива на Фредхолм.
По този начин решението на SLAE по матричния метод се прави по формулата ![]() . Или решението на SLAE се намира с помощта на обратна матрица А -1.
. Или решението на SLAE се намира с помощта на обратна матрица А -1.
Известно е, че квадратна матрица НОпоръчка нна нима обратна матрица А -1само ако неговият детерминант е различен от нула. Така системата нлинейни алгебрични уравнения с ннеизвестните се решават по матричния метод само ако детерминантата на основната матрица на системата не е равна на нула.
Въпреки факта, че има ограничения за възможността за използване на този метод и има изчислителни трудности за големи стойности на коефициентите и системи от висок порядък, методът може лесно да се приложи на компютър.
Пример за решаване на нехомогенна SLAE.

Първо, нека проверим дали детерминантата на матрицата от коефициенти за неизвестни SLAE не е равна на нула.




Сега намираме матрица на съюза, транспонирайте го и го заместете във формулата за определяне на обратната матрица.

Заместваме променливите във формулата:

Сега намираме неизвестните, като умножим обратната матрица и колоната със свободни членове.

Така, х=2; y=1; z=4.
Когато преминавате от обичайната форма на SLAE към матричната форма, внимавайте с реда на неизвестните променливи в системните уравнения. например:

НЕ пишете като:

Необходимо е първо да се подредят неизвестните променливи във всяко уравнение на системата и едва след това да се премине към матричната нотация:


Освен това трябва да внимавате с обозначаването на неизвестни променливи, вместо на x 1 , x 2 , …, x nможе да има и други букви. Например:

в матрична форма пишем:

По-добре е да се решават системи с помощта на матричния метод линейни уравнения, в който броят на уравненията съвпада с броя на неизвестните променливи и детерминантата на основната матрица на системата не е равна на нула. Когато в системата има повече от 3 уравнения, ще са необходими повече изчислителни усилия за намиране на обратната матрица, следователно в този случай е препоръчително да се използва методът на Гаус за решаване.
Системите от уравнения намират широко приложение в икономическата индустрия при математическото моделиране на различни процеси. Например, при решаване на проблеми на управлението и планирането на производството, логистичните маршрути ( транспортна задача) или разполагане на оборудване.
Системите от уравнения се използват не само в областта на математиката, но и във физиката, химията и биологията при решаване на задачи за намиране на размера на популацията.
Система от линейни уравнения е термин за две или повече уравнения с няколко променливи, за които е необходимо да се намери общо решение. Такава последователност от числа, за която всички уравнения стават верни равенства или доказват, че последователността не съществува.
Линейно уравнение
Уравнения от вида ax+by=c се наричат линейни. Означенията x, y са неизвестните, чиято стойност трябва да се намери, b, a са коефициентите на променливите, c е свободният член на уравнението.
Решаването на уравнението чрез начертаване на неговата графика ще изглежда като права линия, всички точки на която са решение на полинома.
Видове системи от линейни уравнения
Най-простите са примери за системи от линейни уравнения с две променливи X и Y.
F1(x, y) = 0 и F2(x, y) = 0, където F1,2 са функции и (x, y) са функционални променливи.
Решете система от уравнения - това означава да се намерят такива стойности (x, y), за които системата се превръща в истинско равенство, или да се установи, че няма подходящи стойности на x и y.
Двойка стойности (x, y), записана като координати на точки, се нарича решение на система от линейни уравнения.
Ако системите имат едно общо решение или няма решение, те се наричат еквивалентни.
Хомогенни системи от линейни уравнения са системи, чиято дясна част е равна на нула. Ако дясната част след знака "равно" има стойност или се изразява с функция, такава система не е хомогенна.
Броят на променливите може да бъде много повече от две, тогава трябва да говорим за пример за система от линейни уравнения с три или повече променливи.
Изправени пред системи, учениците приемат, че броят на уравненията задължително трябва да съвпада с броя на неизвестните, но това не е така. Броят на уравненията в системата не зависи от променливите, може да има произволно голям брой от тях.
Прости и сложни методи за решаване на системи от уравнения
Няма общо аналитичен методрешения на подобни системи, всички методи са базирани на числени решения. Училищният курс по математика описва подробно методи като пермутация, алгебрично събиране, заместване, както и графичния и матричния метод, решението по метода на Гаус.
Основната задача в методите на преподаване на решаване е да се научи как правилно да се анализира системата и да се намери оптималният алгоритъм за решение за всеки пример. Основното нещо е не да запомните система от правила и действия за всеки метод, а да разберете принципите на прилагане на определен метод.
Решаване на примери за системи от линейни уравнения от 7-ми клас на програмата средно училищедоста просто и обяснено много подробно. Във всеки учебник по математика на този раздел се отделя достатъчно внимание. Решението на примери за системи от линейни уравнения по метода на Гаус и Крамер се изучава по-подробно в първите курсове на висшите учебни заведения.
Решаване на системи по метода на заместване
Действията на метода на заместването са насочени към изразяване на стойността на една променлива чрез втората. Изразът се замества в останалото уравнение, след което се свежда до единична променлива форма. Действието се повтаря в зависимост от броя на неизвестните в системата
Нека дадем пример за система от линейни уравнения от 7-ми клас по метода на заместване:

Както може да се види от примера, променливата x е изразена чрез F(X) = 7 + Y. Полученият израз, заместен във 2-рото уравнение на системата на мястото на X, помогна да се получи една променлива Y във 2-рото уравнение . Решение този примерне създава затруднения и ви позволява да получите стойността Y. Последната стъпка е да проверите получените стойности.
Не винаги е възможно да се реши пример за система от линейни уравнения чрез заместване. Уравненията могат да бъдат сложни и изразяването на променливата по отношение на втората неизвестна ще бъде твърде тромаво за по-нататъшни изчисления. Когато в системата има повече от 3 неизвестни, заместващото решение също е непрактично.
Решение на пример за система от линейни нехомогенни уравнения:

Решение с алгебрично събиране
При търсене на решение на системи по метода на събиране се извършва почленно събиране и умножение на уравнения по различни числа. Крайната цел на математическите операции е уравнение с една променлива.

Приложенията на този метод изискват практика и наблюдение. Не е лесно да се реши система от линейни уравнения с помощта на метода на добавяне с брой променливи 3 или повече. Алгебричното събиране е полезно, когато уравненията съдържат дроби и десетични числа.
Алгоритъм за действие на решението:
- Умножете двете страни на уравнението по някакво число. В резултат на аритметичната операция един от коефициентите на променливата трябва да стане равен на 1.
- Добавете получения израз член по член и намерете едно от неизвестните.
- Заменете получената стойност във 2-рото уравнение на системата, за да намерите останалата променлива.
Метод на решение чрез въвеждане на нова променлива
Може да се въведе нова променлива, ако системата трябва да намери решение за не повече от две уравнения, броят на неизвестните също трябва да бъде не повече от две.
Методът се използва за опростяване на едно от уравненията чрез въвеждане на нова променлива. Новото уравнение се решава по отношение на въведеното неизвестно и получената стойност се използва за определяне на оригиналната променлива.

От примера може да се види, че чрез въвеждането на нова променлива t е възможно да се сведе 1-вото уравнение на системата до стандартен квадратен трином. Можете да решите полином, като намерите дискриминанта.
Необходимо е да се намери стойността на дискриминанта по добре познатата формула: D = b2 - 4*a*c, където D е желаният дискриминант, b, a, c са множителите на полинома. В дадения пример a=1, b=16, c=39, следователно D=100. Ако дискриминантът е по-голям от нула, тогава има две решения: t = -b±√D / 2*a, ако дискриминантът е по-малък от нула, тогава има само едно решение: x= -b / 2*a.
Решението за получените системи се намира чрез метода на добавяне.
Визуален метод за решаване на системи
Подходящ за системи с 3 уравнения. Методът се състои в нанасяне на графики на всяко включено в системата уравнение върху координатната ос. Координатите на точките на пресичане на кривите ще бъдат общото решение на системата.
Графичният метод има редица нюанси. Разгледайте няколко примера за решаване на системи от линейни уравнения по визуален начин.

Както се вижда от примера, за всяка линия бяха конструирани две точки, стойностите на променливата x бяха избрани произволно: 0 и 3. Въз основа на стойностите на x бяха намерени стойностите за y: 3 и 0. Точки с координати (0, 3) и (3, 0) бяха отбелязани на графиката и свързани с линия.
Стъпките трябва да се повторят за второто уравнение. Точката на пресичане на линиите е решението на системата.
В следващия пример се изисква да се намери графично решение на системата от линейни уравнения: 0,5x-y+2=0 и 0,5x-y-1=0.

Както се вижда от примера, системата няма решение, тъй като графиките са успоредни и не се пресичат по цялата си дължина.

Системите от примери 2 и 3 са сходни, но когато се конструират, става очевидно, че техните решения са различни. Трябва да се помни, че не винаги е възможно да се каже дали системата има решение или не, винаги е необходимо да се изгради графика.
Матрицата и нейните разновидности
Матриците се използват за кратко записване на система от линейни уравнения. Таблицата се нарича матрица. специален видизпълнени с числа. n*m има n - редове и m - колони.
Матрицата е квадратна, когато броят на колоните и редовете е равен. Матрица-вектор е матрица с една колона с безкрайно възможен брой редове. Матрица с единици по един от диагоналите и други нулеви елементи се нарича идентичност.
Обратна матрица е такава матрица, при умножение на която оригиналната се превръща в единична, такава матрица съществува само за оригиналната квадратна.
Правила за преобразуване на система от уравнения в матрица
По отношение на системите от уравнения, коефициентите и свободните членове на уравненията се записват като числа на матрицата, едно уравнение е един ред от матрицата.
Редът на матрицата се нарича ненулев, ако поне един елемент от реда не е равен на нула. Следователно, ако в някое от уравненията броят на променливите се различава, тогава е необходимо да въведете нула на мястото на липсващото неизвестно.
Колоните на матрицата трябва стриктно да съответстват на променливите. Това означава, че коефициентите на променливата x могат да бъдат записани само в една колона, например първата, коефициентът на неизвестното y - само във втората.
Когато се умножава матрица, всички матрични елементи се умножават последователно по число.
Опции за намиране на обратната матрица
Формулата за намиране на обратната матрица е доста проста: K -1 = 1 / |K|, където K -1 е обратната матрица и |K| - матричен детерминант. |K| не трябва да е равно на нула, тогава системата има решение.
Детерминантата се изчислява лесно за матрица две по две, необходимо е само елементите да се умножат диагонално един по друг. За опцията "три по три" има формула |K|=a 1 b 2 c 3 + a 1 b 3 c 2 + a 3 b 1 c 2 + a 2 b 3 c 1 + a 2 b 1 c 3 + a 3 b 2 c 1 . Можете да използвате формулата или да запомните, че трябва да вземете по един елемент от всеки ред и всяка колона, така че номерата на колоните и редовете на елементите да не се повтарят в продукта.
Решаване на примери за системи от линейни уравнения по матричния метод
Матричният метод за намиране на решение позволява да се намалят тромавите вписвания при решаване на системи с голям брой променливи и уравнения.

В примера a nm са коефициентите на уравненията, матрицата е вектор, x n са променливите, а b n са свободните членове.


Решаване на системи по метода на Гаус
Във висшата математика методът на Гаус се изучава заедно с метода на Крамер, а процесът на намиране на решение на системите се нарича метод за решаване на Гаус-Крамер. Тези методи се използват за намиране системни променливис много линейни уравнения.
Методът на Гаус е много подобен на решенията за заместване и алгебрично събиране, но е по-систематичен. В училищния курс решението на Гаус се използва за системи от 3 и 4 уравнения. Целта на метода е да доведе системата до формата на обърнат трапец. Чрез алгебрични трансформации и замествания стойността на една променлива се намира в едно от уравненията на системата. Второто уравнение е израз с 2 неизвестни, а 3 и 4 - съответно с 3 и 4 променливи.
След привеждане на системата до описания вид, по-нататъшното решение се свежда до последователно заместване на известни променливи в уравненията на системата.
В училищните учебници за 7 клас пример за гаусово решение е описан, както следва:

Както може да се види от примера, на стъпка (3) бяха получени две уравнения 3x 3 -2x 4 =11 и 3x 3 +2x 4 =7. Решението на всяко от уравненията ще ви позволи да намерите една от променливите x n.

Теорема 5, която се споменава в текста, гласи, че ако едно от уравненията на системата бъде заменено с еквивалентно, тогава получената система също ще бъде еквивалентна на оригиналната.
Методът на Гаус е труден за разбиране от учениците гимназия, но е един от най-интересните начини за развитие на изобретателността на децата, записани в програмата задълбочено проучванев часовете по математика и физика.
За по-лесно записване на изчисленията е обичайно да се прави следното:

Коефициентите на уравнение и свободните членове се записват под формата на матрица, където всеки ред от матрицата съответства на едно от уравненията на системата. разделя лявата страна на уравнението от дясната страна. Римските цифри означават номерата на уравненията в системата.
Първо, те записват матрицата, с която да работят, след това всички действия, извършени с един от редовете. Получената матрица се записва след знака "стрелка" и продължава да извършва необходимите алгебрични операции, докато се постигне резултатът.
В резултат на това трябва да се получи матрица, в която един от диагоналите е 1, а всички други коефициенти са равни на нула, тоест матрицата се свежда до единична форма. Не трябва да забравяме да правим изчисления с числата на двете страни на уравнението.
Тази нотация е по-малко тромава и ви позволява да не се разсейвате от изброяване на много неизвестни.
Безплатното прилагане на всеки метод на решение ще изисква грижи и известен опит. Не всички методи се прилагат. Някои начини за намиране на решения са по-предпочитани в определена област на човешката дейност, докато други съществуват с цел обучение.
Тема 2 Решаване на системи от линейни алгебрични уравнения чрез директни методи.
Системите от линейни алгебрични уравнения (съкратено SLAE) са системи от уравнения от вида
или в матрична форма,
А × х = Б , (2.2)
А - матрица на коефициентите на системата от измерения н ´ н
х - вектор от неизвестни, състоящ се от н съставна част
Б - векторът на десните части на системата, състоящ се от н съставна част.
А
=
 х
=
Б
=
(2.3)
х
=
Б
=
(2.3)
Решението на SLAE е такъв набор от н числа, които се заменят със стойности х 1 , х 2 , … , x n в системата (2.1) гарантира, че левите страни са равни на десните във всички уравнения.
Всяка SLAE зависи от стойностите на матриците А и Б Може да се наложи
Едно Решение
Безкрайно много решения
Нито едно решение.
В този курс ще разгледаме само онези SLAE, които имат уникално решение. Необходимо и достатъчно условие за това е детерминантата на матрицата А .
За търсене на решения върху системи от линейни алгебрични уравнения могат да се извършат някои трансформации, които не променят нейните решения. Еквивалентни трансформациисистеми от линейни уравнения се наричат такива негови трансформации, които не променят неговото решение. Те включват:
Пермутация на произволни две уравнения на системата (трябва да се отбележи, че в някои случаи, разгледани по-долу, тази трансформация не може да се използва);
Умножение (или деление) на всяко уравнение на системата с число, което не е равно на нула;
Добавянето към едно уравнение на система от другото й уравнение, умножено (или разделено) по някакво число, различно от нула.
Методите за решаване на SLAE са разделени на две големи групи, наречени - директни методии итеративни методи. Има и начин да се сведе проблема с решаването на SLAE до проблема за намиране на екстремума на функция от няколко променливи, последвано от неговото решаване чрез методи за намиране на екстремума (повече за това, когато преминете през съответната тема). Директните методи осигуряват точното решение на системата (ако съществува) в една стъпка. Итеративните методи (ако е осигурена едновременното им сближаване) позволяват многократно подобряване на някакво първоначално приближение до желаното решение на SLAE и, най-общо казано, те никога няма да дадат точно решение. Въпреки това, като се има предвид, че методите на директни решения също дават не идеално точни решения поради неизбежни грешки при закръгляването на междинните етапи на изчисленията, итеративните методи също могат да осигурят приблизително същия резултат.
Директни методи за решаване на SLAE. Най-често използваните директни методи за решаване на SLAE са:
метод на Крамер,
Метод на Гаус (и неговата модификация - метод на Гаус-Йордан)
Матричен метод (използвайки инверсия на матрица А ).
Метод на Крамер въз основа на изчисляването на детерминанта на основната матрица А и матрични детерминанти А 1 , А 2 , …, A n , които се получават от матрицата А замяна на един в него ( ита) колона ( и= 1, 2,…, н) към колона, съдържаща векторни елементи Б . След това решенията на SLAE се определят като частно от стойностите на тези детерминанти. По-точно, формули за изчислениеима този вид
 (2.4)
(2.4)
Пример 1. Нека намерим по метода на Крамер решението на SLAE, за което
А
=
 , Б
=
.
, Б
=
.
Ние имаме
А 1
=
, A2
=
, А 3
=
,
A4
=
 .
.
Нека изчислим стойностите на детерминантите на всичките пет матрици (използвайки функцията MOPRED на средата превъзхождам). Вземи
Тъй като детерминантата на матрицата А не е равно на нула - системата има уникално решение. След това го дефинираме по формула (2.4). Вземи
Метод на Гаус. Решението на SLAE по този метод включва компилиране на разширена матрица на системата А * . Разширената матрица на системата е матрица с размери нлинии и н+1 колони, включително оригиналната матрица А с колона, прикрепена към нея вдясно, съдържаща вектора Б .
A*
=  (2.4)
(2.4)
Тук a in+1 = b i (i = 1, 2, …, н ).
Същността на метода на Гаус е да се намали (чрез еквивалентни трансформации) на разширената матрица на системата до триъгълна форма (така че само нулеви елементи са под главния й диагонал).
А
*
= 
След това, като се започне от последния ред и се движи нагоре, можем последователно да определим стойностите на всички компоненти на решението.
Началото на трансформациите на разширената матрица на системата до необходимата форма е да видите стойностите на коефициентите при х 1 и избор на реда, в който има максимална абсолютна стойност (това е необходимо, за да се намали големината на изчислителната грешка при последващи изчисления). Този ред от разширената матрица трябва да се замени с първия й ред (или, което е по-добре, да добавите (или извадете) към първия ред и да поставите резултата на мястото на първия ред). След това всички елементи на този нов първи ред (включително тези в последната колона) трябва да бъдат разделени на този фактор. След това новополучения коефициент а 11 става равно на единица. Освен това от всеки от останалите редове на матрицата е необходимо да се извади първия й ред, умножен по стойността на коефициента при х 1 в този ред (т.е. по сумата а и 1 , където и =2, 3, … н ). След това във всички редове, започвайки от втория, коефициентите при х 1 (т.е. всички коефициенти а и 1 (и =2, …, н ) ще бъде нула. Тъй като извършихме само еквивалентни трансформации, решението на новополучената SLAE няма да се различава от оригиналната система.
Освен това, оставяйки първия ред на матрицата непроменен, ще направим всички горни действия с останалите редове на матрицата и в резултат на това с новополучения коефициент а 22 става равно на единица и всички коефициенти а и 2 (и =3, 4, …, н ) ще стане нула. Продължавайки подобни действия, в крайна сметка ще доведем нашата матрица до форма, в която всички коефициенти a ii = 1 (и =1, 2, …, н), и всички коефициенти aij = 0 (и =2, 3, …, н, j< и). Ако на някаква стъпка при търсене на най-голямата абсолютна стойност на коефициента at xj няма да можем да намерим коефициент, който не е равен на нула - това ще означава, че оригиналната система няма уникално решение. В този случай процесът на вземане на решение трябва да бъде прекратен.
Ако процесът на еквивалентни трансформации приключи успешно, тогава получената "триъгълна" разширена матрица ще съответства на следната система от линейни уравнения:

От последното уравнение на тази система намираме стойността x n . Освен това, замествайки тази стойност в предпоследното уравнение, намираме стойността x n -1 . След това, замествайки двете от тези намерени стойности в третото уравнение от дъното на системата, намираме стойността x n -2 . Продължавайки така нататък и се движим по уравнението на тази система отдолу нагоре, последователно ще намерим стойностите на други корени. И накрая, заместване на намерените стойности x n , x n -1 , x n -2 , х 3 и х 2 в първото уравнение на системата намираме стойността х 1 . Такава процедура за търсене на стойностите на корените по намерената триъгълна матрица се нарича наопаки.Процесът на привеждане на оригиналната разширена матрица чрез еквивалентни трансформации до триъгълна форма се нарича в права линияметод на Гаус..
Достатъчно подробен алгоритъм за решаване на SLAE по метода на Гаус е показан на фиг. .2.1 и фиг. 2.1a.
Пример 2. Намерете решението на същата SLAE по метода на Гаус, който вече сме решили по метода на Крамер. Нека първо съставим нейната разширена матрица. Вземи
А
* =
 .
.
Първо, разменяме първия и третия ред на тази матрица (тъй като първата й колона съдържа най-големия елемент в абсолютна стойност) и след това разделяме всички елементи на този нов първи ред на стойността 3. Получаваме
А
* =
 .
.
А
* =

След това разменяме втория и третия ред на тази матрица, разделяме втория ред на пермутираната матрица на 2,3333 и, подобно на горното, задаваме коефициентите във втората колона на третия и четвъртия ред на матрицата на нула. Вземи
А
* =
 .
.
След извършване на подобни действия върху третия и четвъртия ред на матрицата, получаваме
А
* =
 .
.
Разделяйки сега четвъртия ред на -5.3076, завършваме изчертаването на разширената матрица на системата до диагонална форма. Вземи
Ориз. 2.1. Алгоритъм за решаване на системи от линейни алгебрични уравнения по метода на Гаус
 |
|||
Ориз. 2.1a. Макроблок„Изчисляване на стойностите на разтвора“.
А
* =
 .
.
От последния ред веднага получаваме х 4 = 0.7536. Изкачвайки се сега нагоре по редовете на матрицата и извършвайки изчисления, ние последователно получаваме х 3 = 0.7971, х 2 =- 0.1015 и х 1 = 0.3333. Сравнявайки разтвора, получен по този метод, с разтвора, получен по метода на Крамер, е лесно да се провери дали те съвпадат.
Метод на Гаус-Йордан. Този метод за решаване на SLAE е подобен в много отношения на метода на Гаус. Основната разлика е, че с помощта на еквивалентни трансформации разширената матрица на системата от уравнения се свежда не до триъгълна форма, а до диагонална форма, на главния диагонал на която има единици, а извън нея (с изключение на последния н +1 колони) - нули. След завършване на такава трансформация, последната колона на разширената матрица ще съдържа решението на оригиналния SLAE (т.е. x i = а и н +1 (и = 1, 2, … , н ) в получената матрица). Обратното движение (както при метода на Гаус) за окончателните изчисления на стойностите на компонентите на разтвора не е необходимо.
Редуцирането на матрицата до диагонална форма се извършва по принцип, както и по метода на Гаус. Ако на опашка и коефициент при x i (и = 1, 2, … , н ) е малка по абсолютна стойност, тогава низът се търси j , при което коефициентът при x i ще бъде най-голямата по абсолютна стойност това ( j -i) низът се добавя елемент по елемент към и - та линия. След това всички елементи и - тият ред е разделен на стойността на елемента x i Но за разлика от метода на Гаус, след това има изваждане от всеки ред с число j редове с номер и умножено по а джи , но условието j > и заменен с друг. Методът на Гаус-Йордан изважда от всеки ред с число j , и j # и , редове с номер и умножено по а джи . Тези. коефициентите се нулират както под, така и над главния диагонал.
Доста подробен алгоритъм за решаване на SLAE по метода на Гаус – Джордан е показан на фиг. 2.2.
Пример 3. Намерете решението на същата SLAE по метода на Гаус-Джордан, който вече сме решили по методите на Крамер и Гаус.
Напълно подобно на метода на Гаус, ние съставяме разширената матрица на системата. След това разменяме първия и третия ред на тази матрица (тъй като първата й колона съдържа най-големия елемент с абсолютна стойност) и след това разделяме всички елементи на този нов първи ред на стойността 3. След това изваждаме от всеки ред на матрица (с изключение на първия) елементите от първия ред, умножени по коефициента в първата колона на този ред. Получаваме същото като при метода на Гаус
А
* =
 .
.
След това разменяме втория и третия ред на тази матрица, разделяме втория ред на пренаредената матрица на 2,3333 и ( вече за разлика от метода на Гаус) задайте коефициентите във втората колона на първия, третия и четвъртия ред на матрицата на нула. Вземи
Пример 1. Намерете общо решение и някакво конкретно решение на систематаРешениенаправи го с калкулатор. Изписваме разширените и главни матрици: 
Пунктираната линия разделя основната матрица A. Неизвестните системи записваме отгоре, като се има предвид възможната пермутация на членовете в уравненията на системата. Определяйки ранга на разширената матрица, ние едновременно намираме ранга на основната. В матрица B първата и втората колона са пропорционални. От двете пропорционални колони само една може да попадне в основния минор, така че нека преместим, например, първата колона отвъд пунктираната линия с противоположен знак. За системата това означава прехвърляне на членове от x 1 в дясната страна на уравненията. 
Привеждаме матрицата в триъгълна форма. Ще работим само с редове, тъй като умножаването на ред от матрица по ненулево число и добавянето му към друг ред за системата означава умножаване на уравнението по същото число и добавянето му към друго уравнение, което не променя решението на системата. Работа с първия ред: умножете първия ред на матрицата по (-3) и добавете на свой ред към втория и третия ред. След това умножаваме първия ред по (-2) и го добавяме към четвъртия. 
Вторият и третият ред са пропорционални, следователно един от тях, например вторият, може да бъде зачеркнат. Това е еквивалентно на изтриване на второто уравнение на системата, тъй като то е следствие от третото. 
Сега работим с втория ред: умножете го по (-1) и го добавете към третия. 
Прекъснатият минор има най-висок ред (от всички възможни минори) и е различен от нула (равен е на произведението на елементите на главния диагонал), като този минор принадлежи както на основната матрица, така и на разширената матрица, следователно rangA = ранг B = 3 .
Незначителен  е основно. Той включва коефициенти за неизвестни x 2, x 3, x 4, което означава, че неизвестните x 2, x 3, x 4 са зависими, а x 1, x 5 са свободни.
е основно. Той включва коефициенти за неизвестни x 2, x 3, x 4, което означава, че неизвестните x 2, x 3, x 4 са зависими, а x 1, x 5 са свободни.
Преобразуваме матрицата, оставяйки само основния минор отляво (което съответства на точка 4 от горния алгоритъм за решение). 
Системата с коефициенти на тази матрица е еквивалентна на оригиналната система и има формата

x 4 =3-4x 5 , x 3 =3-4x 5 -2x 4 =3-4x 5 -6+8x 5 =-3+4x 5
x 2 =x 3 +2x 4 -2+2x 1 +3x 5 = -3+4x 5 +6-8x 5 -2+2x 1 +3x 5 = 1+2x 1 -x 5
Получихме отношения, изразяващи зависими променливи x 2, x 3, x 4 през свободни x 1 и x 5, тоест намерихме общо решение:

Давайки произволни стойности на свободните неизвестни, получаваме произволен брой конкретни решения. Нека намерим две конкретни решения:
1) нека x 1 = x 5 = 0, тогава x 2 = 1, x 3 = -3, x 4 = 3;
2) поставете x 1 = 1, x 5 = -1, след това x 2 = 4, x 3 = -7, x 4 = 7.
Така намерихме две решения: (0.1, -3,3,0) - едно решение, (1.4, -7.7, -1) - друго решение.
Пример 2. Проучете съвместимостта, намерете общо и едно конкретно решение на системата 
Решение. Нека пренаредим първото и второто уравнение, така че да има единица в първото уравнение и да напишем матрицата B. 
Получаваме нули в четвъртата колона, работеща на първия ред: 
Сега вземете нулите в третата колона, като използвате втория ред: 
 Третият и четвъртият ред са пропорционални, така че един от тях може да бъде зачеркнат, без да се променя ранга:
Третият и четвъртият ред са пропорционални, така че един от тях може да бъде зачеркнат, без да се променя ранга:
Умножете третия ред по (-2) и добавете към четвъртия: 
Виждаме, че ранговете на основната и разширените матрици са 4, а рангът съвпада с броя на неизвестните, следователно системата има уникално решение:
-x 1 = -3 → x 1 \u003d 3; x 2 = 3-x 1 → x 2 = 0; x 3 \u003d 1-2x 1 → x 3 = 5.
x 4 \u003d 10- 3x 1 - 3x 2 - 2x 3 = 11.
Пример 3. Проверете системата за съвместимост и намерете решение, ако съществува. 
Решение. Ние съставяме разширената матрица на системата. 
 Пренаредете първите две уравнения, така че да има 1 в горния ляв ъгъл:
Пренаредете първите две уравнения, така че да има 1 в горния ляв ъгъл:
Умножавайки първия ред по (-1), добавяме го към третия: 
Умножете втория ред по (-2) и добавете към третия: 
Системата е непоследователна, тъй като основната матрица получава ред, състоящ се от нули, който се зачерква при намиране на ранга, а последният ред остава в разширената матрица, тоест r B > r A .
Упражнение. Изследвайте тази система от уравнения за съвместимост и я решете с помощта на матрично смятане.
Решение
Пример. Докажете съвместимостта на система от линейни уравнения и я решите по два начина: 1) по метода на Гаус; 2) Метод на Крамер. (въведете отговора във формата: x1,x2,x3)
Решение :doc :doc :xls
Отговор: 2,-1,3.
Пример. Дадена е система от линейни уравнения. Докажете неговата съвместимост. Намерете общо решение на системата и едно конкретно решение.
Решение
Отговор: x 3 \u003d - 1 + x 4 + x 5; x 2 \u003d 1 - x 4; x 1 = 2 + x 4 - 3x 5
Упражнение. Намерете общи и конкретни решения за всяка система.
Решение.Изучаваме тази система с помощта на теоремата на Кронекер-Капели.
Изписваме разширените и главни матрици:
| 1 | 1 | 14 | 0 | 2 | 0 |
| 3 | 4 | 2 | 3 | 0 | 1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
| х 1 | x2 | х 3 | x4 | x5 |
Тук матрицата А е с удебелен шрифт.
Привеждаме матрицата в триъгълна форма. Ще работим само с редове, тъй като умножаването на ред от матрица по ненулево число и добавянето му към друг ред за системата означава умножаване на уравнението по същото число и добавянето му към друго уравнение, което не променя решението на системата.
Умножете 1-вия ред по (3). Умножете 2-рия ред по (-1). Нека добавим 2-ри ред към 1-ви:
| 0 | -1 | 40 | -3 | 6 | -1 |
| 3 | 4 | 2 | 3 | 0 | 1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Умножете 2-рия ред по (2). Умножете третия ред по (-3). Нека добавим 3-ия ред към 2-рия:
| 0 | -1 | 40 | -3 | 6 | -1 |
| 0 | -1 | 13 | -3 | 6 | -1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Умножете 2-рия ред по (-1). Нека добавим 2-ри ред към 1-ви:
| 0 | 0 | 27 | 0 | 0 | 0 |
| 0 | -1 | 13 | -3 | 6 | -1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Избраният минор има най-висок ред (от всички възможни минорни) и е различен от нула (равен е на произведението на елементите на реципрочния диагонал), като този минор принадлежи както на основната матрица, така и на разширената матрица, следователно rang(A ) = rang(B) = 3 Тъй като рангът на основната матрица е равен на ранга на разширената, тогава системата е съвместна.
Този минор е основен. Включва коефициенти за неизвестни x 1, x 2, x 3, което означава, че неизвестните x 1, x 2, x 3 са зависими (основни), а x 4, x 5 са свободни.
Преобразуваме матрицата, оставяйки само основния минор отляво.
| 0 | 0 | 27 | 0 | 0 | 0 |
| 0 | -1 | 13 | -1 | 3 | -6 |
| 2 | 3 | -3 | 1 | -3 | 2 |
| х 1 | x2 | х 3 | x4 | x5 |
27x3=
- x 2 + 13x 3 = - 1 + 3x 4 - 6x 5
2x 1 + 3x 2 - 3x 3 = 1 - 3x 4 + 2x 5
По метода на елиминиране на неизвестните намираме:
Получихме отношения, изразяващи зависими променливи x 1, x 2, x 3 през свободни x 4, x 5, тоест открихме общо решение:
х 3 = 0
x2 = 1 - 3x4 + 6x5
x 1 = - 1 + 3x 4 - 8x 5
несигурен, защото има повече от едно решение.
Упражнение. Решете системата от уравнения.
Отговор:x 2 = 2 - 1,67x 3 + 0,67x 4
x 1 = 5 - 3,67 x 3 + 0,67 x 4
Давайки произволни стойности на свободните неизвестни, получаваме произволен брой конкретни решения. Системата е несигурен
матрична форма
Системата от линейни уравнения може да бъде представена в матрична форма като:

или според правилото за умножение на матрици,
Ах = Б.Ако към матрицата A се добави колона от свободни термини, тогава A се нарича разширена матрица.
Методи за решение
Директните (или точните) методи ви позволяват да намерите решение в определен брой стъпки. Итеративните методи се основават на използването на повтарящ се процес и ви позволяват да получите решение в резултат на последователни приближения
Директни методи
- Метод на почистване (за тридиагонални матрици)
- Метод на разлагане на Холески или квадратен корен (за положително определени симетрични и ермитови матрици)
Итеративни методи
Решаване на система от линейни алгебрични уравнения във VBA
Опция Explicit Sub rewenie() Dim i As Integer Dim j Като цяло число Dim r() Като Double Dim p Като Double Dim x() Като Double Dim k Като цяло число Dim n Като цяло число Dim b() Като Double Dim файл Като цяло число Dim y () Като двоен файл = FreeFile Отворете "C:\data.txt" За въвеждане като файл Input #file, n ReDim x(0 To n * n - 1 ) Като Double ReDim y(0 To n - 1 ) Като Double ReDim r(0 до n - 1 ) Като двойно за i = 0 до n - 1 За j = 0 до n - 1 Вход #файл, x(i * n + j) Следващ j Вход #файл, y(i) Следващ i Затворете #file За i = 0 до n - 1 p = x(i * n + i) За j = 1 до n - 1 x(i * n + j) = x(i * n + j) / p Следващо j y (i) = y(i) / p За j = i + 1 до n - 1 p = x(j * n + i) За k = i До n - 1 x(j * n + k) = x(j * n + k) - x(i * n + k) * p Следващо k y(j) = y(j) - y(i) * p Следващо j Следващо i „ Горна триъгълна матрицаЗа i = n - 1 до 0 Стъпка -1 p = y(i) За j = i + 1 до n - 1 p = p - x(i * n + j) * r(j) Следващо j r(i) = p / x(i * n + i) Следващ i " Назад за i = 0 До n - 1 MsgBox r(i) Следващ i "край под
Вижте също
Връзки
Бележки
Фондация Уикимедия. 2010 г.
Вижте какво е "SLAU" в други речници:
СЛАУ- система от линейни алгебрични уравнения ... Речник на съкращенията и съкращенията
Този термин има други значения, вижте Slough (значения). Град и единна единица на Slough Engl. Slough Country ... Уикипедия
- (Слау) град в Обединеното кралство, част от индустриалния пояс около Голям Лондон, на железопътна линияЛондон Бристол. 101,8 хил. жители (1974 г.). Машиностроене, електрическо, електронно, автомобилно и химическо ... ... Голяма съветска енциклопедия
Слау- (Слау) Слау, индустриален и търговски град в Бъркшир, юг. Англия, западно от Лондон; 97 400 жители (1981 г.); леката промишленост започва да се развива в периода между световните войни ... Държави от света. Речник
Слау: Слау е град в Англия, в графство Бъркшир SLAU Система от линейни алгебрични уравнения ... Wikipedia
Комуна Рьослау Рьослау Герб ... Уикипедия
Град Бад Вьослау Бад Вьослау Герб ... Уикипедия
Проекционните методи за решаване на SLAE са клас итеративни методи, при които проблемът за проектиране на неизвестен вектор върху определено пространство се решава оптимално по отношение на друго пространство. Съдържание 1 Постановка на проблема ... Wikipedia
Град Бад Вьослау Бад Фьослау Държава АвстрияАвстрия ... Уикипедия
Фундаменталната система от решения (FSR) е набор от линейно независими решения на хомогенна система от уравнения. Съдържание 1 Хомогенни системи 1.1 Пример 2 Хетерогенни системи ... Wikipedia
Книги
- Преки и обратни задачи на реконструкция на изображение, спектроскопия и томография с MatLab (+CD), Сизиков Валерий Сергеевич. Книгата описва използването на апарата от интегрални уравнения (IU), системи от линейни алгебрични уравнения (SLAE) и системи от линейно-нелинейни уравнения (SLNU), както и софтуерни инструменти ...